Область - абсолютная устойчивость
Cтраница 2
Если выделить какой-либо параметр цепи q и считать его комплексным, то граница области абсолютной устойчивости на плоскости q определяется уравнением W ( q; jcct) 0 при изменении со от 0 до оо. Такая граница разделяет плоскость q на разные области и для того, чтобы определить, какая из них является областью абсолютной устойчивости, надо проверить выполнение условия абсолютной устойчивости ( 4 - 42) для одной точки каждой из этих областей. В действительности параметр цепи q является вещественным, поэтому следует рассматривать лишь вещественную составляющую области абсолютной устойчивости. [16]
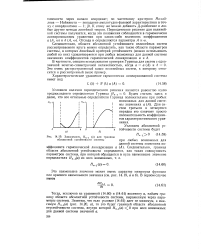 |
Зависимость Нп ( а для границы абсолютной УСТОЙЧИВОСТИ системы. [17] |
Тогда, исключив из уравнений (14.60) и (14.61) величину а, найдем границу области абсолютной устойчивости системы, выраженную через параметры системы. [18]
Однако использование функций сопротивления и проводимости может приводить к различным результатам при определении расположения области абсолютной устойчивости относительно этой границы. [19]
Неправильный выбор функции сопротивления вместо проводимости, или наоборот, не вис-сит ошибки при определении границы области абсолютной устойчивости на оси параметра цепи, ко может привести к неправильному определению положения этой области относительно границы. [20]
Таким образом, использование функций сопротивления или проводимости приводит к одинаковым результатам при определении величин, соответствующих границе области абсолютной устойчивости. [21]
Метод основан на построении вариационным способом некоторой вспомогательной предельной системы - наихудшей с точки зрения близости к границе области абсолютной устойчивости. Из асимптотической устойчивости по отношению к части переменных такой предельной системы следует абсолютная устойчивость по всем переменным исходной системы. В работе Е.С. Пятницкого и Л.Б. Рапопорта [1991] указанный подход распространен на более общие случаи. [22]
Таким образом, использование функций сопротивления или проводимости всегда приводит к одинаковому значению дг параметра цепи, которое соответствует границе области абсолютной устойчивости. [23]
Для того чтобы избежать этого ограничения и чтобы выбор шага определялся лишь соображениями точности решения, при решении жестких задач Коши используются так называемые А-устойчивые методы [238] с неограниченной в левой полуплоскости областью абсолютной устойчивости. [24]
Область G значений hA на комплексной плоскости, допускающую значения А 0, при которых все решения разностной схемы в применении к задаче (7.28) при Re А 0 стремятся к нулю, если п - оо, называют областью абсолютной устойчивости данной схемы. Говорят также, что разностная схема абсолютно устойчива в области О. [25]
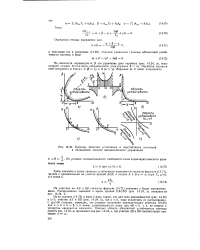 |
Границы областей устойчивых и неустойчивых состояний в нелинейной системе автоматического управления. [26] |
Поэтому область абсолютной устойчивости системы ( вместо рис. 14.24, а) принимает вид рис. 14.24, в, где участки ЛР и Во, соответствуют значению а со. [27]
Такие методы называют А-устойчивыми методами. Методы, у которых область абсолютной устойчивости ограничена в левой полуплоскости, называются ограниченно устойчивыми методами. [28]
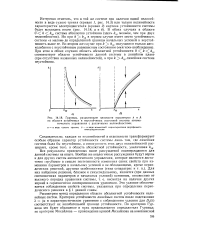 |
Границы, разделяющие плоскости параметров k и А на области устойчивых и неустойчивых состояний системы автоматического управления с различными нелинейностями. [29] |
Но при k klp в первом случае имеет место устойчивость системы в малом до определенной границы начальных условий и неустойчивость выше ее. При этом в обоих случаях область абсолютной устойчивости 0 k k2 соответствует области устойчивости данной системы в линейном плане ( при отсутствии названных нелинейностей), а при k kzp линейная система неустойчива. [30]
Страницы: 1 2 3