Область - хаос
Cтраница 1
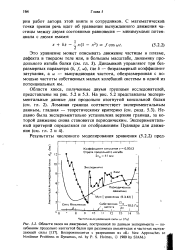
Области хаоса, полученные двумя группами исследователей, представлены на рис. 5.2 и 5.3. На рис. 5.2 представлены экспериментальные данные для продольно изогнутой консольной балки ( см. гл. Ломаная граница соответствует экспериментальным данным, гладкая - теоретическому критерию ( см. разд. Недавно была экспериментально установлена верхняя граница, за которой движение снова становится периодическим. [2]
Область хаоса не является однородной. [3]
 |
Стохастический слой в окрестности сепаратрисы нелинейного маятника. [4] |
Область хаоса точно локализована. Ее носителем является окрестность сепаратрисы. Далее будет видно, что сделанное утверждение обладает значительной степенью универсальности. [5]
В области хаоса эти торы разрушены. Очевидно, в трехмерном фазовом пространстве ( и в четырехмерном на трехмерной поверхности пост, энергии) области хаотического и регулярного поведения разделены. Если фазовое пространство имеет размерность больше четырех, то геом. Обычно это происходит вдоль сепаратрис ( етохастич. [6]
В области хаоса наблюдаются узкие окна, где колебания являются периодическими с периодом, равным трем, пяти и семи периодам внешней силы. [7]
В области хаоса спектральная плотность процесса x ( t), точечное отображение и проекция фазового портрета показаны на рис. 9.21 г 5, 9.22 5 и 9.23, е соответственно. [8]
Показано, что в области хаоса точечное отображение сводится к одномерному, имеющему гладкий максимум. [9]
Сосуществование в фазовом пространстве областей устойчивой динамики и областей хаоса является одним из самых удивительных и неожиданных открытий. Оно позволяет проанализировать, как зарождается хаос и как выглядит минимальная область хаоса. И хотя на многие вопросы здесь еще нет ответов, тем не менее, сейчас ясно, что зародышем хаоса является стохастический слой, образующийся в окрестности разрушенных сепаратрис. Стохастический слой был описан в работе [1] при изучении задачи об устойчивости и разрушении магнитных поверхностей, а в [2] были получены различные оценки его ширины. Эта глава будет посвящена систематическому анализу стохастического слоя и некоторым важным приложениям ( ком. Образование стохастического слоя при возмущении нелинейного маятника является типичным. Поэтому эта модель будет рассмотрена первой. [10]
Как показали численные расчеты, переходы из областей синхронизации в область хаоса происходят по-разному в зависимости от амплитуды внешнего воздействия. [11]
Один из интересных вопросов, возникающих в связи с возможностью сосуществования области хаоса и области и устойчивости: как устроена граница хаоса. [12]
Полученные результаты представлены па рис. 9.8, где сплошными линиями показаны периодические режимы, а косой штриховкой - область хаоса. Горизонтальными линиями внутри области хаоса показан режим утроения периода, а вертикальными - упятерения. Зависимости области бифуркаций и хаотических колебаний от параметра у для ряда значений а показаны на рис. 9.9, Hrf которого видно, что при увеличении область сложного поведения системы смещается в сторону более высоких частот. [13]
 |
Зависимость числа вращения от k и Д / 2. г в виде трехмерного графика. [14] |
Чем больше знаменатель рационального числа вращения w p / q, тем ближе к критической линии k 1 располагается в данном языка Арнольда область хаоса. В пределе q - оо, что соответствует иррациональным числам вращения, хаос можно обнаружить сколь угодно близко к критической линии. [15]
Страницы: 1 2 3