Область - хаос
Cтраница 3
Иногда точка CQO называется точкой Фейгенбаума. В диапазоне между с 1 / 4 и COQ удвоение периода присходит по мере того как с - CQO. Другой участок, где с CQQ, иногда называется областью хаоса. [31]
 |
Стохастическая паутина линий тока с квазисимметрией 5-го порядка. Плоскость z 0. Решение уравнений соответствует q 5 и е 0 03. Размер квадрата 24тгХ24я. [32] |
Полученный результат показывает, что в пространстве ( х, у, z) имеется конечная область - паутина, толщиной порядка е, внутри которой линии тока располагаются в пространстве стохастически. Хотя этот вывод здесь приведен лишь для частного случая гексагональной симметрии, он может быть достаточно просто обобщен на случай АВС-течения [21] или течения с произвольной квазисимметрией. Это означает, что стационарные течения, создавая определенную структуру в пространстве, одновременно порождают области хаоса расположения линий тока толщиной порядка б в окрестности этой структуры. Трехмерный характер структур для образования структурного хаоса является необходимым условием. [33]
По периферии рисунка показаны фазовые портреты аттрактора, отвечающие некоторым характерным точкам пространства параметров. Замечательно, что для этой автономной системы дифференциальных уравнений основные элементы на карте динамических режимов те же самые, какие были отмечены для отображений. Это области периодичности, разграниченные линиями бифуркаций удвоения периода, перекрестки с характерным расположением линий складок и точек сборки, сложная структура границы хаоса с присутствием узких областей регулярной динамики, простирающихся вдоль линий складок далеко в область хаоса. [34]
В работе [210] получены некоторые универсальные закономерности при малом внешнем периодическом воздействии на систему, описываемую одномерным точечным отображением типа параболы. Показано, что с ростом величины воздействия значения бифуркационного параметра цп, соответствующие ге-й бифуркации удвоения периода, монотонно растут. В случае нерезонансного воздействия найденные значения ц соответствуют бифуркациям удвоения квазипериода тора. Отметим, что распространение полученных результатов на область хаоса, возможно, позволит объяснить наличие порога синхронизации и его связь с положительным ляпуновским показателем. [35]
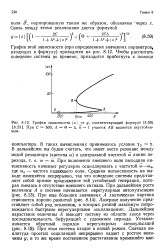 |
График зависимости х от у, соответствующий формуле. [36] |
При включении внешнего поля выходная интенсивность начинает регулярно осциллировать с частотой со-со, где со0 - частота падающего поля. Средняя интенсивность на выходе изменяется непрерывно, так что поведение системы представляет собой прямое продолжение той устойчивой генерации, которая имелась в отсутствие внешнего сигнала. Лазерное излучение представляет собой ряд всплесков, в которых резкий максимум сопровождается быстрыми нерегулярными осцилляциями. Дальнейшее нарастание величины А выводит систему из области хаоса через последовательность бифуркаций с удвоением периода. При этом система входит в новый режим. [37]
 |
Пример круговой шкалы взаимодействий. [38] |
Напротив, в случае черно-белых шкал компенсации противоположных отношений не происходит: при уменьшении интенсивности отношения R сила отношения R - не возрастает, и наоборот. Здесь принцип дополнительности не работает: по мере удаления от краев шкалы оценки обоих отношений - как R, так и R становятся все более неопределенными. Более того, срединная точка подобной шкалы есть точка разрыва, в которой нет ни того, ни другого отношения 1 ( R V R), т.е. наблюдается максимальная неопределенность. С позиций синергетики окрестность этой точки можно интерпретировать как область хаоса, в которой возможно спонтанное возникновение нового смысла в результате веерного перехода с одной шкалы на другие. [39]
Даже еслиЛ о 1 периодические по t возмущения дают тот же результат. Хотя существование области стохастичности и становится, таким образом, некоторым универсальным свойством динамических систем, это еще не означает сильной неустойчивости в системе. Причина такого утверждения заключается в том, что области хаоса очень узкие. Поэтому дальнейшая судьба стохастических траекторий определяется тем, как соединяются области хаоса между собой или, иначе, тем, какова топология слабого хаоса в фазовом пространстве. [40]
В определенном смысле эта точка является границей хаоса: при А Ас реализуется только регулярное, периодическое поведение, а для А Ас в сколь угодно малой окрестности критической точки существуют значения параметра, отвечающие хаосу. В области устойчивых периодических движений ляпуновский показатель отрицателен. В точках бифуркаций удвоения периода он подходит к нулю. За точкой накопления каскада удвоений периода зависимость ляпуновского показателя от параметра имеет сложный характер, причем чередуются области хаоса с положительными его значениями и периодических режимов, для которых он отрицателен. [41]
В заключение отметим работу [38], посвященную анализу структуры бифуркационной диаграммы для динамических систем, содержащих седловое состояние равновесия, неустойчивое многообразие которого состоит из двух симметричных одномерных сепаратрис. Примером может служить система галеркинских уравнений, описывающая режимы тепловой конвекции в поле вибрации при слабом нарушении инверсионной симметрии. Рассмотрена ситуация, когда возникающие в системе го-моклинные петли являются притягивающими. В области регулярного поведения обнаружены, помимо периодических, квазипериодические режимы, которым соответствуют инвариантные множества канторотора Граница области хаоса оказывается фрактальной. [42]
На рис. 10.5 представлена бифуркационная диаграмма логистического уравнения. На график нанесены возможные величины х, соответствующие различным константам а. Из графика видно, что несмотря на хаотичность системы, имеет место определенная упорядоченность в ее возможных решениях. На нижний уровнях а существуют единичные равновесные решения. Видны также точки бифуркаций и область хаоса между значениями а, равными 0.90 и 1.0. Но даже в хаотической области наблюдается некий порядок. [43]
Ранее мы познакомились с ситуацией, в которой сколь угодно малое возмущение приводит к образованию областей фазового пространства, внутри которых динамика системы является стохастической. Однако хаос неустраним, если только выполнены некоторые общие условия относительно размерности системы. В некотором не очень строгом смысле можно назвать случай, когда области стохастической динамики очень малы, случаем слабого хаоса. Как бы малы ни были области хаоса, их существование означает принципиальную неинтегрируемосгь системы. [44]
Страницы: 1 2 3