Область - хаос
Cтраница 2
Каждой такой точке соответствует один резонанс, и каждому такому резонансу соответствует стохастический слой, создающий на плоскости ( coj, со2) малу область хаоса. При е - 0 размеры областей стремдтся к нулю, и они не пересекаются. [16]
Пример зависимости v от k показан на рис. 9.112. Как и следовало ожидать, в области периодических колебаний v 1, в области квазипериодических, соответствующих двумерному тору, v 2, в области хаоса величина v плавно нарастает с ростом А, начиная от значения, равного двум. [17]
 |
Бифуркационная диаграмма ( бифуркационное дерево для логистического отображении. [18] |
При достаточно больших А наблюдается хаос, соответствующие области выглядят как более или менее равномерно заполненные точками участки кроны. Области хаоса чередуются с окнами устойчивости - узкими зонами по параметру, в которых динамика становится периодической. [19]
 |
Схема кольцевого генератора Дмитриева-Кислова. [20] |
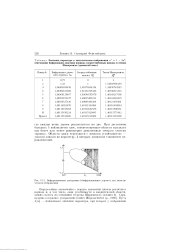
По периферии приведены фазовые портреты аттракторов, отвечающих нескольким представительным точкам пространства параметров. В области хаоса имеются окна периодических режимов характерной формы. На карте можно также усмотреть структуру типа перекрестка, которая содержит точку сборки и линии складок. [21]
На бифуркационной диаграмме ( рис. 9.14) они характеризуются числом ге, равным числу оборотов за период внешней силы. В области хаоса число оборотов и направление вращения от периода к периоду могут изменяться. [22]
Полученные результаты представлены па рис. 9.8, где сплошными линиями показаны периодические режимы, а косой штриховкой - область хаоса. Горизонтальными линиями внутри области хаоса показан режим утроения периода, а вертикальными - упятерения. Зависимости области бифуркаций и хаотических колебаний от параметра у для ряда значений а показаны на рис. 9.9, Hrf которого видно, что при увеличении область сложного поведения системы смещается в сторону более высоких частот. [23]
График этой функции представлен на рис. 5.6 вместе с результатами физических и численных экспериментов. Критерий (5.3.25) дает очень точную нижнюю границу областей хаоса на плоскости амплитуда - частота вынуждающей силы. [24]
 |
Схематическое изображение части плоскости параметров нелинейной системы, отвечающей области crossroad - перекресток.| Иллюстрация гистерезиса, наблюдаемого в окрестности точки сборки. [25] |
С каждым из них ассоциируется определенный лист карты динамических режимов, на котором имеется своя конфигурация областей, отвечающих метаморфозам этого аттрактора. В частности, на каждом листе представлены линии бифуркаций удвоения периода, области хаоса, а также вторичные сборки и вторичные перекрестки, организованные около этих сборок. [26]
При достижении границ цикл начинает изгибаться и претерпевать бифуркации. Численно обнаружены бифуркации удвоения цикла, приводящие к хаосу. Области хаоса на рис. 9.99 заштрихованы горизонтальными линиями. [27]
Странный аттрактор, определяющий хаотическое поведение системы, часто занимает ограниченную область фазового пространства. Поэтому, хотя траектории разбегаются с экспоненциальной скоростью, убежать за границы странного аттрактора они не могут. Следовательно, определение границ области хаоса может позволить получить оценки поведения системы. [28]
При Ске 0 9; 1 1933 ] ( 5 5 9) было зафиксировано несколько устойчивых и неустойчивых периодических движений, причем при увеличении Сх период устойчивых движений удваивался. Значения Сх в таблице 9.8 выбраны в области хаоса. [29]
Даже еслиЛ о 1 периодические по t возмущения дают тот же результат. Хотя существование области стохастичности и становится, таким образом, некоторым универсальным свойством динамических систем, это еще не означает сильной неустойчивости в системе. Причина такого утверждения заключается в том, что области хаоса очень узкие. Поэтому дальнейшая судьба стохастических траекторий определяется тем, как соединяются области хаоса между собой или, иначе, тем, какова топология слабого хаоса в фазовом пространстве. [30]
Страницы: 1 2 3