Плоская область

Cтраница 3

Аппарат квазиконформных отображений плоских областей ( с двумя парами характеристик) может быть привлечен также в качестве теоретич. [31]

Тогда каждая из плоских областей D представляет собой треугольник или параллелограмм. [32]

Пусть граница dG ограниченной плоской области G состоит из конечного числа простых кусочно-гладких контуров. [33]

На рис. 21.10 изображена плоская область, составленная из треугольников. Каждый треугольник является конечным элементом, имеющим свой порядковый номер. Общие вершины треугольных конечных элементов называются узлами, которые также нумеруются. Граница области представляет собой ломаную линию. Кинематические граничные условия задаются в узлах на границе. [34]

Какова бы ни была плоская область D и каково бы ни было непрерывное распределение в ней характеристик р, 6, существует квазиконформное отображение области D с этими характеристиками, определенное с точностью до конформного отображения. [35]

В коротких цилиндрах наблюдается плоская область разрушения НК, параллельная основанию цилиндра. Она вызвана отражением импульса от плоского торца цилиндра и подобна образованию откола в плоских пластинках. На рисунке показан луч PGH, иллюстрирующий образование этого разрушения. [36]

Настоящая глава посвящена изучению плоских областей наложения. В следующей главе мы рассмотрим римановы области общего вида. [37]

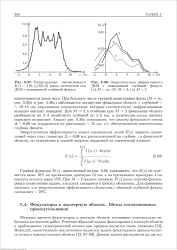Распределение интенсивности Рис, Энергетическая эффективность I ( z - J ( 0, z / I ( 0 0 вдоль оптической оси ДОЭ с глубиной фокуса. [38]

Методам расчета фокусаторов в плоскую область посвящено относительно небольшое количество работ. [39]

Для дифференциальных форм на плоских областях аналогичное утверждение, вообще, неверно. [40]

Если G и D - плоские области, их евклидовы границы гомеоморфны окружности и D ограничена, то для функций /, аналитических в G, выполняется С. Кроме этой, в практике конформных отображений используются и другие формы С. [41]

В том случае, когда плоская область Q ограничена эллипсом, такая координатная система хорошо известна - это общий случай эллиптических координат. Семейство софокусных эллиптических цилиндров, образующие которых параллельны оси у, позволяет рассмотреть случай плоской области Q, представляющей полосу в плоскости ху, ограниченную двумя прямыми, параллельными оси у. При этом следует рассматривать вместо (2.8) логарифмический потенциал простого слоя. [42]

Действительно, в таком случае общая плоская область для обоих углов трения есть такой треугольник Р АВ ( фиг. [43]

Это свойство аналогично свойству односвязности плоской области; при наличии его пространственную область ( Т) также называют ( поверхностно)) односвязной. Упомянем для примера, что тело, ограниченное двумя концентрическими сферическими поверхностями, будет в этом смысле односвязным, а тор нет. [44]

Далее для сечений стержней как плоских областей понадобятся их геометрические характеристики. [45]

Страницы: 1 2 3 4