Связная область

Cтраница 2

Любую n - связную область можно представлять себе как односвязную область, в которой прорезано п - 1 дырок. [16]

Лабиринт разбивает плоскость на связные области. [17]

Пусть / w - связная область D ограничена кривыми Со ( внешняя граница) и С, С. [18]

Теорема 5.11. Пусть конечно связная область D на z - сфере содержит начало и бесконечно удаленную точку. Пусть b - внутренняя точка D, отличная от нуля и бесконечности. [19]

Теорема 6.13. Пусть конечно Связная область D на z - сфере содержит бесконечно удаленную точку. [20]

Фундаментальная группа m - связной области D является свободной группой cm - 1 образующими. [21]

В качестве модулей n - связной области D можно взять и другие ц действительных параметров ( ц - 1, если 7i2, и ( Л - Зп - 6, если ге3), определяющих конформное отображение области D на нек-рую канонич. [22]

Аналогично определяется метрика рц в произвольной связной области U. [23]

Если жидкость, занимающая дву связную область, ограниченную твердыми стенками, совершает ациклическое движение, то движение мгновенно прекращается, если границы приводятся в состояние покоя. Однако если движение является циклическим, то циклическая часть будет сохраняться при остановке границ. [24]

Пусть D является m - связной областью. [25]

Это - ограниченная одн - - связная область. [26]

Теорема 2.5. Пусть D - дву связная область плоскости w, ни одна из граничных, компонент которой не вырождается в точку. Пусть Г - класс локально спрямляемых кривых, лежащих в области D и соединяющих ее граничные компоненты. [27]

Таким образом, для n - связных областей из всех возможных комбинаций причинности допустимы только две: когда все е-переменные являются входами в n - связную область или когда все е-переменные являются выходами из нее. Это соответствует тому, что все уравнения разрешены относительно / - либо е-переменных. [28]

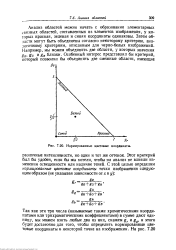Нормированные цветовые координаты. [29]

Анализ областей можно начать с образования элементарных связных областей, составленных из элементов изображения, у которых красная, зеленая и синяя координаты одинаковы. Затем области могут быть объединены согласно некоторому критерию, аналогичному критериям, описанным для черно-белых изображений. Например, мы можем объединить две области, у которых значения § R, SG и gB близки. [30]

Страницы: 1 2 3 4