Обращение - скорость
Cтраница 3
При нашем подходе ( в отличие ных значения от больцмановского) эффект корреляций при переопределении - функции сохраняется. Следовательно, в точке обращения скоростей о функция Ж должна претерпевать скачок, поскольку мы внезапно создаем в этой точке аномальные пред-столкновительные корреляции, которые должны нарушиться позднее. Скачок - функции соответствует энтропии, или информационной цене, которую нам приходится платить. [32]
Нельзя не отметить еще одно важное обстоятельство: при t tu новая Ж - функция принимает два различных значения, одно - для системы до обращения скоростей, другое - для системы после обращения скоростей. Энтропия системы до обращения и после обращения скоростей различна. Это напоминает ситуацию, происходящую при преобразовании пекаря, когда сжимающийся и растягивающийся слои - скорости, переходящие друг в друга при обращении. [33]
Это предположение относительно начального состояния газа известно под названием гипотезы молекулярного хаоса. Начальное состояние, возникающее в результате обращения скоростей, не удовлетворяет гипотезе молекулярного хаоса. Если систему заставить эволюционировать вспять во времени, то создается новая ситуация, аномальная в том смысле, что некоторым молекулам, сколь бы далеко друг от друга они ни находились в момент обращения скоростей, предопределено встретиться в заранее установленный момент времени и подвергнуться заранее установленному преобразованию скоростей. [34]
Канонические уравнения обратимы: обращение времени математически эквивалентно обращению скорости. Канонические уравнения консервативны: гамильтониан, выражающий полную энергию системы в канонических переменных ( координатах и импульсах), сохраняется при изменениях координат и импульсов во времени. [35]
Следует сказать несколько слов относительно граничных условий в задачах этого типа. Во-первых, здесь необходимы обычные условия непрерывности температур и тепловых потоков и обращение скорости в нуль на границе с твердым телом. Что касается условий, налагаемых на электромагнитное поле, то, поскольку внешнее электрическое поле отсутствует, в жидкости будет протекать только индуктированный электрический ток по замкнутым контурам параллельно поверхности пластины и перпендикулярно на правлению движения жидкости. [36]
Предположим, что, прежде чем производить обращение скоростей, мы достаточно долго выжидаем. В этом случае послестолкновительные корреляции имели бы произвольный радиус и энтропийная цена за обращение скоростей была бы непомерно велика. [37]
Это - основная симметрия классической динамики, и можно было бы надеяться, что кинетическое уравнение Больцмана, описывающее, как изменяется во времени функция распределения, обладает такой же симметрией. Но в действительности все обстоит иначе: вычисленный Больцманом столкновительный член инвариантен относительно обращения скорости. Эта несколько неожиданная инвариантность имеет простой физический смысл: в больцмановской картине нет никакого различия между столкновением, обращенным в будущее, и столкновением, обращенным в прошлое. Именно на этой идее основано возражение Пуанкаре против вывода уравнения Больцмана, предложенного самим Больцманом. Но, как мы видели, симметрия кинетического уравнения, выведенного Больцманом для функции распределения, противоречит симметрии классической динамики. Следовательно, заключает Пуанкаре, Больцман не сумел вывести энтропию из динамики. Где-то в своих рассуждениях он ввел нечто новое, чуждое динамике. Следовательно, выведенное Больцманом уравнение в лучшем случае может рассматриваться лишь как феноменологическая модель, полезная, но не имеющая прямого отношения к динамике. Таково было также возражение Цер-мело ( 1896), выдвинутое против теории Больцмана. [38]
Предположим, что, прежде чем производить обращение скоростей, мы достаточно долго выжидаем. В этом случае послестолкновитель-ные корреляции имели бы произвольный радиус и энтропийная цена за обращение скоростей была бы непомерно велика. [39]
Все изложенное выше предполагает, что для рассматриваемого случая обтекания наперед задано распределение скоростей U ( x) на внешней границе пограничного слоя. Вспомним, что теоретическое распределение скорости, получаемое из условия безвихревого обтекания крылового профиля идеальной жидкостью, приводит к полному восстановлению давления и обращению скорости в нуль на задней кромке профиля. При этом, как показывают предыдущие формулы, величины /, 8, 8 обращаются в бесконечность. [40]
Указанные результаты носят в основном диагностический характер, поскольку решение (5.7) относится к стационарному режиму. При этом нужно учитывать закономерности ее суточных колебаний ( Бер-лянд, 1947; Buajitti, Blackedar, 1957; Матвеев, 1984; Орленко, 1979 и др.), согласно которым на определенном уровне происходит так называемое обращение скорости ветра. Ниже этого уровня максимум скорости ветра достигается днем, а минимум - ночью, а выше, наоборот, максимум достигается ночью, а минимум - днем. [41]
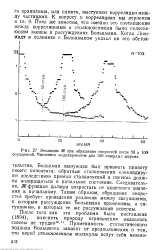 |
Эволюция Ш при обращении скоростей после 50 и 100 соударений. Численное моделирование для 100 твердых шаров. [42] |
Больцман вынужден был признать правоту своего оппонента: обратные столкновения ликвидируют последствия прямых столкновений и система должна возвращаться в начальное состояние. Следовательно, - функция должна возрастать от конечного значения к начальному. Таким образом, обращение скоростей требует проведения различия между ситуациями, К которым рассуждения Больцмана применимы, и ситуациями, в которых те же рассуждения неверны. [43]
Применимость статистического подхода Больцмана зависит от предположения о том, что перед столкновением молекулы ведут себя независимо друг от друга. Это предположение относительно начального состояния газа известно под названием гипотезы молекулярного хаоса. Начальное состояние, возникающее в результате обращения скоростей, не удовлетворяет гипотезе молекулярного хаоса. [44]
Наиболее серьезным из них, по-видимому, является парадокс об обратимости, сформулированный Лошмидтом. Сущность этого парадокса сводится к следующему: при обращении скоростей молекул система должна вернуться в исходное состояние. [45]
Страницы: 1 2 3 4