Обращение - скорость
Cтраница 1
Обращение скоростей порождает высокоорганизованную систему, и гипотеза молекулярного хаоса перестает выполняться. [1]
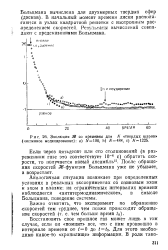 |
Эволюция 3 со временем для N твердых шаров ( численное моделирование. а 100, Ь 484, с 1225. [2] |
После обращения скоростей - функция Больцмана уже не убывает, а возрастает. [3]
Для обращения скоростей к молекулам извне должна поступить информация. Для того чтобы обратить скорости, необходимо существо, аналогичное демону Максвелла, а за демона Максвелла приходится платить. При нашем подходе ( в отличие от больцманов-ского) эффект корреляций при переопределении 5 -фуик-ции сохраняется. [5]
После обращения скоростей - функция Больцмана уже не убывает, а возрастает. [6]
Найдем границу области обращения скорости у в нуль, представляющую собой кривую переключений реле; для этого из уравнений ( 76) и ( 85) определим точечное преобразование у ( х) полупрямой Ljj используя уравнения ( 76) и ( 85), получим ( см фиг. [7]
Однако имеется объяснение этого обращения скоростей реакцииг при котором рассматривается изменение положения переходного состояния вдоль реакционной координаты по мере изменения относительных энергий реагентов, переходного состояния и продуктов реакции. Для удобства обсуждения предположим, что обе рассматриваемые реакции протекают от исходных реагентов до продуктов реакции через стадии двух переходных состояний, как это показано на рис. 16 ( стр. Эти реакционные пути представлены на рис. 18 и 19, причем рис. 18 иллюстрирует реакцию с метилатом, а рис. 19-реакцию с пиперидином. Предполагается, что тетраэдрические промежуточные соединения имеют геометрические строения XXVII ( стр. Промежуточные соединения в реакциях с метилатом должны иметь значительно более низкое содержание энергии, чем в реакциях с пиперидином, в которых имеются разделенные заряды. [8]
Больцманом столкновительный член инвариантен относительно обращения скорости. Эта несколько неожиданная инвариантность имеет простой физический смысл: в болыщановской картине пет никакого различия между столкновением, обращенным в будущее, и столкновением, обращенным в прошлое. Именно на этой идее основано возражение Пуанкаре против вывода уравнения Больцмана, предложенного самим Больцма-иом. Но, как мы видели, симметрия кинетического-уравнения, выведенного Больцманом для функции распределения, противоречит симметрии классической динамики. Следовательно, заключает Пуанкаре, Больц-ман не сумел вывести энтропию из динамики. Где-то-в своих рассуждениях он ввел нечто новое, чуждое динамике. Следовательно, выведенное Больцманом уравнение в лучшем случае может рассматриваться лишь как феноменологическая модель, полезная, но не имеющая прямого отношения к динамике. Таково было также возражение Цермело ( 1896), выдвинутое против теории Больцмана. [9]
Скорости точек струны при этом обращении скорости точки излома назад остаются непрерывными. [10]
Предположим, что, прежде чем производить обращение скоростей, мы достаточно долго выжидаем. В этом случае послестолкновительные корреляции имели бы произвольный радиус и энтропийная цена за обращение скоростей была бы непомерно велика. [11]
Предположим, что, прежде чем производить обращение скоростей, мы достаточно долго выжидаем. В этом случае послестолкновитель-ные корреляции имели бы произвольный радиус и энтропийная цена за обращение скоростей была бы непомерно велика. [12]
Ясно, что эти распределения удовлетворяют условиям обращения скорости на поверхности и в окружающей среде в нуль и температуры соответственно в t0 и too. Кроме того, на границе пограничного слоя г / б равны нулю градиенты скорости и температуры. [13]
Ясно, что эти распределения удовлетворяют условиям обращения скорости на поверхности ив окружающей среде в нуль и температуры соответственно в / о и too. Кроме того, на границе пограничного слоя у б равны нулю градиенты скорости и температуры. [14]
Нужно поставить естественное в данной задаче условие - обращение скорости в нуль на бесконечности. [15]
Страницы: 1 2 3 4