Оператор - эволюция
Cтраница 1
Операторы эволюции U ( T) и U ( T) по-прежнему находятся по формулам (4.2.30), но теперь второй оператор выражается через резольвенту R ( z), так как матрица W не эрмитова. [1]
Парциальный оператор эволюции не может быть унитарным, поскольку он описывает только один эволюции. Полная ( единичная) вероятность распределяется в этом случае по разным каналам, и только сумма по всем каналам соответствует полной ( единичной) вероятности. [2]
Термин оператор эволюции обычно употребляется в приложениях, где ф ( описывает изменение состояния некоторой реальной физической системы во времени. Термин поток чаще употребляется в случае, когда изучается динамика в целом, а не эволюция данной конкретной точки. [3]
Если оператор эволюции во времени является унитарным, то U U 1, и мы видим, следовательно, что нам не удалось создать полосы, воздействуя вторым импульсом. Еще удивительнее, если бы смогла работать какая-нибудь другая схема, разработанная для восстановления интерференционных полос. Тем не менее, наличие информации, содержащейся в трехуровневых атомах, аналогично обладанию информацией, хранящейся в виде результатов наблюдения, а известно, что процесс наблюдения изменяет вектор состояния неунитарным образом. Более наглядно вопрос можно поставить так: можно ли стереть информацию ( память), запертую в атомах, и таким образом восстановить полосы. Под влиянием этих рассуждений, рассмотрим следующее стирающее ( информацию) устройство. [4]
Здесь оператор эволюции ехр г. ( 1 - Pq) L действует на все динамические переменные, расположенные справа от него. [5]
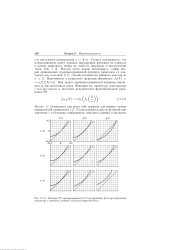 |
Действие РГ преобразования на функцию f ( x при значениях параметра е меньшем, равном и большем критического. [6] |
Она задает перенормированный оператор эволюции за два временных шага. [7]
Экспериментальная реализация операторов эволюции f / p и Um зависит от исследуемой системы. [8]
Поскольку в критической точке операторы эволюции за 2fc и 2 шагов идентичны с точностью до замены масштаба динамической переменной на фактор се, то и структура аттрактора должна воспроизводить себя при таком пересчете масштаба. [10]
Однако такой простой вид оператор эволюции имеет только для линейных уравнений. Действительно, знание оператора фг эквивалентно умению решать уравнение (1.53), и поэтому определение оператора встречает такие же трудности. [11]
Такую же роль играет оператор эволюции на плоскости. [12]
Отсюда видим, что оператор эволюции во времени является произведением экспоненциальных операторов. Но так как операторы не обязательно коммутируют, мы не можем просуммировать показатели экспонент. Это возможно только в том случае, когда гамильтонианы H ( tv) в разные моменты времени tv коммутируют. [13]
Далее нетрудно построить все операторы эволюции общей теории, описывающие поведение системы в постоянном внешнем поле. [14]
Структура выражения (15.11) для оператора эволюции во времени достаточно прозрачна: динамика атомно-полевой системы определяется четным или нечетным числом актов обмена квантом возбуждения между полем и атомом, которым и соответствуют два вклада в эту формулу. [15]
Страницы: 1 2 3 4
