Определение - размерность
Cтраница 2
Результат определения размерности физической величины принято записывать условным равенством, в котором эта величина заключается в квадратные скобки. [16]
По определению размерности в М существуют т линейно независимых элементов. Поскольку они являются элементами пространства Лп, то тем самым в Rn существуют т линейно независимых элементов. [17]
При определении размерностей тепловых величин обычно не используют связь между температурой и энергией движения молекул; температура рассматривается как одна из основных единиц системы. Единицей измерения температуры служит градус; величина градуса зависит от применяемой температурной шкалы. По наиболее распространенной международной стоградусной шкале градус представляет собой сотую часть температурного интервала, отсчитанного от точки таяния льда до точки кипения воды, измеренных при нормальном давлении. [18]
При определении размерностей тепловых величин обычно не используют связь между температурой и энергией движения молекул; температура рассматривается как одна из основных единиц системы. Единицей измерения температуры служит град-ус; величина градуса зависит от применяемой температурной шкалы. По наиболее распространенной международной стоградусной шкале градус представляет собой сотую часть температурного интервала, отсчитанного от точки таяния льда до точки кипения воды, измеренных при нормальном давлении. [19]
Попытаемся исправить определение размерности, приняв во внимание разную вероятность посещения ячеек покрытия. Для этого следует привлечь конструкцию, обсуждавшуюся в лекции 8, - инвариантную меру. [20]
Что касается определения размерности, то Урысон чуть позже определил ее иным ( эквивалентным) способом: фигура S имеет размерность п, если ее можно разбить на сколь угодно малые замкнутые части так, что ни одна точка S не принадлежит п 2 различным частям, но при достаточно мелком разбиении есть точки, принадлежащие п 1 различным частям. [21]
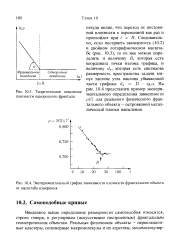 |
Теоретическое поведение плотности однородного фрактала.| Экспериментальный график зависимости плотности фрактального объекта от масштаба измерения. [22] |
Введенное выше определение размерности самоподобия относится, строго говоря, к регулярным ( искусственно построенным) фрактальным геометрическим объектам. [23]
Простейший способ определения размерности Минковского фрактала А состоит в следующем. [24]
Существует несколько принципиально разных определений размерности геометрического объекта. Топологическая размерность множества всегда выражается целым числом; это не противоречит интуитивному представлению о том, что кривые одномерны, а поверхности двумерны. Размерность Хаусдорфа лежит в основе фрактальной теории. Размерность Минковского может служить аналогом размерности Хаусдорфа, удобным для использования в прикладных задачах. Эти размерности, как правило, совпадают, но алгоритм определения размерности Минковского намного эффективнее. [25]
По самому определению размерности ясно, что по данным трем независимым единицам коэфициенты приведения всех других величин могут быть выражены в коэфициентах, соответствующих этим трем величинам. [26]
Заменим в определении хаусдорфовой размерности класс покрытий. [27]
Если при определении размерности физической величины составляющие ее основные единицы измерения сокращаются, то такая величина называется безразмерной. Безразмерными величинами являются относительные координаты точек тела, аэродинамические коэффициенты профиля крыла, относительные деформации упругой конструкции. Постоянные и переменные безразмерные величины занимают особое место при изучении подобия физических явлений. [28]
Центральное место в определении размерности Хаусдорфа-Безиковича и, следовательно, фрактальной размерности D занимает понятие расстояния между точками в пространстве. [29]
Как и при определении поточечной размерности, непрерывная траектория дискре гизируется - заменяется множеством из N точек [ х ] в фазовом пространстве. [30]
Страницы: 1 2 3 4