Определитель - квадратная матрица
Cтраница 2
Определителем квадратной матрицы называется определитель, составленный из элементов матрицы, расположенных так же, как и в матрице. [16]
Определителем квадратной матрицы ( или просто определителем) называют число, которое вычисляется по определенным правилам из элементов этой матрицы. [17]
Определителем квадратной матрицы называется определитель, составленный из элементов матрицы, расположенных так же, как и в матрице. [18]
Если определитель квадратной матрицы Л - з 0, то она называется вырожденной. Для любой невырожденной матрицы [ Л ] существует обратная матрица [ Л ] - 1 такая, что [ Л ] Х [ Л ] - 1 [ / ], где [ / ] - единичная матрица. [19]
Если определитель квадратной матрицы не равен нулю, то матрица называется неособенной, в противном случае - особенной. [20]
Вандермонда ( определитель квадратной матрицы порядка п в левой части уравнения) отличен от нуля. Случай кратных собственных значений является более сложным. [21]
Для вычисления определителя квадратной матрицы А следует: с помощью цепного алгоритма преобразовать данную матрицу А в верхнюю треугольную матрицу В; вычислить произведения диагональных элементов матрицы В. [22]
Рассмотрим вычисление определителя невырожденной квадратной матрицы с выбором максимальных элементов ( см. § 3, стр. [23]
Следствие 17.6. Если определитель квадратной матрицы равен нулю, то ее строки ( столбцы) линейно зависимы. [24]
Подпрограмма позволяет вычислить определитель квадратной матрицы методом Гаусса. [25]
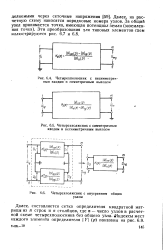 |
Четырехполюсник с несимметричным входом и симметричным выходом.| Четырехполюсник с симметричным входом и несимметричным выходом.| Четырехполюсник с внутренним общим узлом. [26] |
Далее, составляется сетка определителя квадратной матрицы из п строк и п столбцов, где га - число узлов в расчетной схеме четырехполюсника без общего узла. [27]
Напишите фортран-подпрограмму, которая вычисляет определитель квадратной матрицы А порядка п из разложения, вычисленного подпрограммой DECOMP. Используйте логарифмы, как предложено в § 3.3, или какой-нибудь другой прием, чтобы избежать переполнений и машинных нулей. [28]
Таким образом, для вычисления определителя квадратной матрицы необходимо привести ее к треугольному виду и найти произведение ее диагональных элементов. При этом следует учесть, что выбор главного элемента осуществляется перестановкой строк матрицы, каждая из перестановок изменяет знак определителя на противоположный. [29]
Сложность переадресации в программе вычисления определителя невырожденной квадратной матрицы вызвана тем, что число циклов по параметру i - переменное. [30]
Страницы: 1 2 3