Ошибка - усечение
Cтраница 1
Ошибка усечения оценивается в зависимости от степени гладкости функции f ( x следующим образом. [1]
Ошибка усечения той же формулы оценивается величиной М3 / 12 / 6, где М3 - наибольшее значение / ( х) в рассматриваемом интервале. [2]
При этом ошибка усечения составляет 1 / 3 суммарной ошибки, а 2 / 3 ее приходится на ошибку округления. [3]
В совокупности ошибки усечения и округления могут вызвать более серьезные последствия, чем можно было бы ожидать, особенно когда величины, участвующие в вычислениях, имеют различные порядки, и порядки величин, округленных на предыдущих шагах вычислений, больше, чем на последующих. [4]
В некотором смысле ошибка усечения - это цена, которую мы платим за привилегию использования целочисленной двоичной арифметики. Одно из ее проявлений - ошибка, вносимая при использовании усечения в процессе деления на целую степень двойки. Допустим, например, что мы имеем значение 31, представленное пятибитовым двоичным числом 1 1 1.1 12, и мы хотим разделить его на 16, используя сдвиг битов на Т 4 позиции вправо и игнорируя ( отсекая) сдвинутые биты. Ошибка деления с усечением составляет здесь почти 50 % правильного ответа. Если бы исходное делимое было равно 63 и представлено шестибитовым двоичным числом 1 1 1 1 1 12, то деление его на 1 6 путем сдвига вправо на четыре бита дало бы нам двоичный результат 0000 1 1 2, или 3 Q. [5]
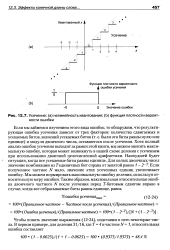 |
Усечение. ( а нелинейность квантования. ( Ь функция плотности вероятности ошибки. [6] |
Хотя полный анализ ошибок усечения выходит за рамки этой книги, мы можем оценить максимальную ошибку, которая может возникнуть в нашей схеме деления с усечением при использовании двоичной целочисленной арифметики. Наихудшей будет ситуация, когда все усекаемые биты равны единице. Если полученное частное N мало, значение этих усеченных единиц увеличивает ошибку. [7]
 |
Сравнение алгоритмов aMax /. Min. [8] |
Для схем Max / JMin ошибки усечения являются функцией длины слова данных, используемого алгоритма, значений / и Q и угла вектора. [9]
Если требуется улучшение сходимости и допустима ошибка усечения порядка О ( / г3), то можно получить величину s, равную нулю. [10]
Если требуется улучшение сходимости и допустима ошибка усечения порядка О ( Л3), то можно получить величину s, равную нулю. [11]
Чтобы улучшить сходимость метода Крэнка и Ни-кольсона без увеличения ошибки усечения [ как это было для ( 236) и ( 237) ] и порядка уравнений в конечных разностях [ 48, разд. Эти методы основываются на последовательных подстановках, аналогичных используемым в методе Рунге-Кутта [ 25, стр. [12]
Чтобы улучшить сходимость метода Крэнка и Ни-кольсона без увеличения ошибки усечения [ как это было для ( 236) и ( 237) ] и порядка уравнений в конечных разностях [ 48, разд. Эти методы основываются на последовательных подстановках, аналогичных используемым в методе Рунге - Кутта [ 25, стр. [13]
Здесь ошибка округления оценивается величиной 4е / Л2, а ошибка усечения - величиной ftaM4 / 12, где М4 - наибольшее значение / ( 4) ( х) в рассматриваемом интервале. [14]
Они могут быть выбраны из условия, обеспечивающего определенный компромисс между малой ошибкой усечения и высокой степенью сходимости. [15]
Страницы: 1 2 3