Перебор - параметр
Cтраница 1
Перебор параметров и численное интегрирование производятся на ЭВМ. [1]
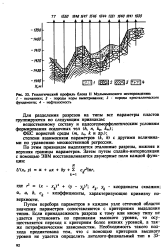 |
Геологический профиль блока II Мулымьинского месторождения. [2] |
Путем перебора параметров в каждом узле сеточной области значения параметров сопоставляются с критериями выделения типов. Если принадлежность разреза к тому или иному типу не удается установить по признакам высокого уровня, то осуществляется переход к критериям более низких уровней, а также петрофизическим зависимостям. [3]
После многократного перебора параметров пласта на модели и совпадения расчетных давлений на скважинах с фактическими он позволяет производить оценку запасов газа и приближенно параметров пласта. [4]
В большинстве задач электромеханики при наличии математической модели1 необходимо путем перебора параметров ЭП отыскать оптимальные показатели при определенном сочетании параметров. Как уже отмечалось, изменение одного параметра при неизменных других не дает возможности найти нужные соотношения и требует больших затрат машинного времени. Метод ПЭ позволяет правильно провести эксперимент и обеспечивает уменьшение числа опытов. [5]
В большинстве задач элепромеханики при наличии математической модели необходимо путем перебора параметров ЭП отыскать оптимальные показатели при определенном сочетании параметров. Как уже отмечалось, изменение одного параметра при неизменных других не дает возможности найти нужные соотношения и требует больших затрат машинного времени. Метод ПЭ позволяет правильно провести эксперимент и обеспечивает уменьшение числа опытов. [6]
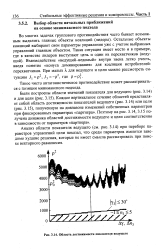 |
Область достижимости показателя ведущего. [7] |
Анализ области показателя ведущего ( см. рис. 3.14) при переборе параметров управлений цели показал, что среди параметров имеются заведомо худшие решения, которые не имеет смысла рассматривать при поиске векторного равновесия. [8]
Для отыскания очередного второго параметра проверки производится расчет вероятностей отказа второго перебора параметров, при этом из расчета исключаются те группы элементов, которые были проверены при контроле параметра уи. В конкретном случае исключаются из расчета вероятности отказов элементов аь й8, а12 и аи. [9]
Расчетами определялся градиент давления, необходимый для движения газожидкостной смеси по трубам с внутренним диаметром 62 мм, во всех вариантах перебора параметров, указанных выше. [10]
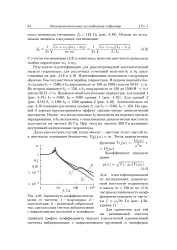 |
Зависимость коэффициентов передач от частоты. 1 - гидроопоры. 2 - классическая. 3 - резиновый виброизолятор, одномассовая система виброизоляции с параллельными пружиной и демпфером. [11] |
Результаты идентификации для рассматриваемой математической модели гидроопоры для различных сочетаний величин Ь и Ъ % представлены на рис. 4.18 и 4.19. Идентификацию выполняли следующим образом. Был осуществлен перебор параметров. На кривой 3 хорошо просматривается эффект размягчения динамической жесткости. Видно, что когда значение Ь находится на верхнем пределе варьирования, а 62 на нижнем, то наименьшая динамическая жесткость получается на частоте 25 Гц. При этом на частоте 200 Гц возникает внутренний антирезонанс гидроопоры. [12]
Указанные условия ( 1) легко реализуются программным путем. Это и послужило причиной того, что была организована программа для перебора параметров ходьбы ( начального расположения ног и режима их работы) и последующей проверки этих начальных расположений на сохранение устойчивости в течение всего цикла ходьбы. [13]
В настоящее время для решения конкретных задач оптимизации ионообменных процессов применяются в основном экспериментальные методы. При небольшом числе переменных ( 2 - 3) определение оптимальных условий достаточно точно и быстро достигается методом перебора параметров, получения зависимости критерия оптимальности от одной варьируемой переменной при фиксированных значениях остальных. Выбор наилучшего варианта из числа рассматриваемых является результатом такого поиска. Изменение значений фиксированных ранее параметров требует новой серии экспериментов для нахождения оптимума. Использование широко распространенного метода планирования, эксперимента [1] позволяет сократить число экспериментов, необходимых для определения оптимума критерия оптимальности, и одновременно находить его значение при изменении всех варьируемых параметров. В этом методе на основании экспериментальных данных получают зависимость критерия оптимальности от варьируемых параметров процесса в виде полиномов, производится статистическая обработка и оценка коэффициентов полученных уравнений, определяется минимум ( максимум) критерия оптимальности. [14]
Точно так же, как и при обратном трассировании лучей, модель объекта состоит из сплошных объемных тел и тонких участков поверхностей. Сохраняются структура описания объекта и булево выражение, моделирующее объект. Теперь же форма представления поверхности должна быть параметрической: XX ( s t); YY ( s t); ZZ ( s t), что позволяет перебором параметров s t вычислять координаты серии точек на поверхности. При достаточной густоте точек их изображение полностью передает образ самой поверхности. [15]
Страницы: 1 2