Задача - штурма-лиувилль
Cтраница 1
Задача Штурма-Лиувилля называется регулярной, если интервал [ а, Ь ] конечен и функция q ( x) на этом интервале суммируема. [1]
Задача Штурма-Лиувилля ( 1) имеет бесконечное ( счетное) число собственных значений. [2]
Но задача Штурма-Лиувилля имеет ряд специфических свойств. [3]
Свойства задачи Штурма-Лиувилля ( 5) подробно описаны в разд. Там же приведены асимптотические и приближенные формулы для собственных значений и собственных функций. [4]
Рассмотрим задачу Штурма-Лиувилля для оператора Лапласа на единичной сфере. [5]
Теорема 5.1. Задача Штурма-Лиувилля (5.7) эквивалентна интегральному уравнению (5.12) с симметричным замкнутым ядром. [6]
Теорема 5.2. Задача Штурма-Лиувилля (5.7) имеет бесконечное число ( последовательность) собственных значений. [7]
Собственные функции задачи Штурма-Лиувилля обладают рядом замечательных свойств, которые широко используются не только при решении краевых задач для обыкновенных дифференциальных уравнений, но и при решении краевых задач для уравнений в частных производных, а также для решения многих других математических проблем. Большинство этих свойств можно проще всего доказать путем сведения краевой задачи (4.73), (4.74) к интегральному уравнению Фредгольма второго рода с симметричным ядром. [8]
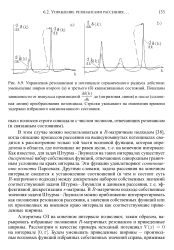 |
Управления резонансами в потенциале ограниченного радиуса действия. уменьшение ширин второго ( а и третьего ( б квазисвязанных состояний. Показаны. [9] |
Как известно, для задач Штурма-Лиувилля на таких интервалах существует дискретный набор собственных функций, отвечающих однородным граничным условиям на краях интервала. Эти функции удовлетворяют соотношению полноты Парсеваля. [10]
Теорема 5.4. Каждое собственное значение задачи Штурма-Лиувилля (5.7) имеет ранг, равный единице. [11]
В следующем параграфе мы изучим задачу Штурма-Лиувилля в более общем виде, чем (5.5), и установим свойства ее собственных значений и собственных функций. [12]
Теперь мы можем доказать, что задача Штурма-Лиувилля эквивалентна нахождению собственных функций некоторого интегрального оператора с непрерывным симметрическим ядром. [13]
Можно доказать, что собственные числа и собственные функции задачи Штурма-Лиувилля при наличии указанных выше особенностей имеют в соответственных промежутках те же свойства, какие были указаны для основной задачи. [14]
Математическое подкрепление картины опирается на сведение задачи путем нелинейной замены к задаче Штурма-Лиувилля Lu и с неким линейным дифференциальным оператором L и нулевыми условиями на бесконечности. [15]
Страницы: 1 2 3