Сопряженная задача

Cтраница 1

Сопряженная задача существенно упрощается при больших значениях критерия Пекле. Рассмотрим, как и ранее, два предельных случая: без учета и с учетом циркуляции внутри капли. [1]

Сопряженная задача имеет комплексно сопряженные собственные значения той же кратности. [2]

Подобные сопряженные задачи, включающие электрические, диффузионные и тепловые процессы, характерны для многих коррозионных явлений и обусловлены сложной зависимостью кинетики коррозионного процесса от переменных физико-химических свойств контактирующей с металлом среды. [3]

Сопряженные задачи конвективного теплообмена имеют большое значение для исследования химико-технологических процессов. [4]

Сопряженную задачу можно рассматривать как задачу, поставленную для зеркальной системы, или антисистемы, процессы в которой протекают в обращенном времени. [5]

Решение сопряженной задачи (4.1) - (4.14) в общем виде получить не представляется возможным, поэтому авторы некоторых работ прибегают к различным допущениям. [6]

Исследование сопряженных задач требует проведения экспериментов. Поэтому наряду с совершенствованием методов решения сопряженных задач необходимо изучать и обобщать зависимости нестационарной теплопередачи для типичных законов изменения граничных условий. Специфика теплообмена низкотемпературных сжиженных газов проявляется большей частью в процессах теплоотдачи, сопровождающихся изменением агрегатного состояния, как-то: кипением, испарением, конденсацией. Например, процессы кипения наблюдаются при заполнении резервуаров и трубопроводов, а процессы испарения и конденсации - при эксплуатации резервуаров. Уметь анализировать процессы теплообмена необходимо для рациональной эксплуатации оборудования процессов хранения и транспорта сжиженных газов. [7]

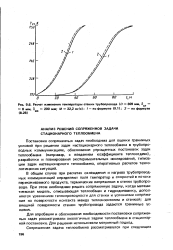Расчет изменения температуры стенки трубопровода ( О 309 мм, 5 8 мм, § 200 мм. М - 32 2 кг / с. 1 - по формуле. 2 - по формуле из. [8]

Постановка сопряженных задач необходима для оценки граничных условий при решении задач нестационарного теплообмена в трубопроводных коммуникациях, обоснования упрощенных постановок задач теплообмена ( например, с введением коэффициента теплоотдачи), разработки и планирования экспериментальных исследований, типизации задач нестационарного теплообмена, оперативных расчетов технологических ситуаций. [9]

Решение сопряженных задач теплообмена связано с преодолением принципиальных математических трудностей. Основная трудность состоит в том, что приходится решать систему уравнений в частных производных, имеющих различный вид на разных интервалах; в случае стационарных задач мы сталкиваемся даже с дифференциальными уравнениями разных типов: для жидкости получается уравнение в частных производных параболического типа, а для твердого тела - эллиптического типа. Наиболее рациональным подходом к решению сопряженных задач является введение на границе сопряжения неизвестной функции, равной температуре или тепловому потоку на этой границе, которое позволяет свести систему уравнений в частных производных к двум несвязанным краевым задачам. Неизвестная функция определяется в дальнейшем из оставшихся условий сопряжения. [10]

Решение сопряженных задач теплообмена связано с преодолением принципиальных математических трудностей. Основная трудность состоит в том, что приходится решать систему уравнений в частных производных, имеющих различный вид на разных интервалах, в случае стационарных задач мы сталкиваемся даже с дифференциальными уравнениями разных типов: для жидкости получается уравнение в частных производных параболического типа, а для твердого тела-эллиптического типа. Наиболее рациональным подходом к решению сопряженных задач является введение на границе сопряжения неизвестной функции, равной температуре или тепловому-потоку на этой границе, которое позволяет свести систему уравнений в частных производных к двум несвязанным краевым задачам. Неизвестная функция определяется в дальнейшем из оставшихся условий сопряжения. [11]

Решение сопряженных задач подобного рода удается получить только в простейших случаях. При наперед заданных граничных условиях решается отдельно диффузионная задача, а затем определяется суммарное термическое сопротивление. [12]

Рассмотрим сопряженную задачу, т.е. задачу Коши в пространствах аналитических функционалов. И здесь случаи цилиндрической и конической эволюции особенностей решения принципиально различны. Если в первом случае как прямая, так и сопряженная задачи легко укладываются в рамки исследования дифференциальных уравнений в банаховом пространстве v ( t) - Au ( t) h ( t), где A ( t) - ограниченный оператор, то при конической эволюции соответствующая абстрактная задача Коши не сводится к известным схемам для дифференциально-операторных уравнений. В этом случае оператор A ( t) имеет переменную область определения и, следовательно, для исследования требуются новые подходы. [13]

Рассмотрим сопряженную задачу поток - стенка. Так как расход считаем известным, то замкнутая система уравнений является граничным условием второго рода для уравнения теплопроводности стенки. В упрощенном варианте расчета принимаем, что стенка трубы достаточно тонкая, что позволит пренебречь распределением температуры по толщине стенки и перетечками тепла по ее длине. [14]

Рассмотреть сопряженную задачу теплообмена, схема которой показана на рис. 17 5.1 8, предполагая, что речь идет о керамической пластине, находящейся в воздухе. Считая, что включен лишь нижний нагреватель, расположенный в точке xL 0 25, определить максимальную температуру поверхности и долю подводимой энергии, которая теряется за счет - теплопроводности к пластине. [15]

Страницы: 1 2 3 4