Вторичная периодичность

Cтраница 2

Таким образом, вторичная периодичность связана непосредственно с заполнением в атомах d - и / - подуровней, приводящим к упрочнению связи внешних s - и / 7-электронов с ядром. Так как первоначальное заполнение d - подуровня наблюдается в атомах элементов четвертого периода, а / - подуровня - - в атомах элементов шестого периода, то скачок в изменении свойств должен быть особенно заметен при переходе от элементов третьего периода к четвертому и от элементов пятого периода к элементам шестого периода. В целом вторичная периодичность обусловлена структурой электронных оболочек атомов и в скрытой форме отображается в периодической системе элементов. [16]

Примечательно, что вторичная периодичность сильнее всего проявляется в свойствах соединений химических элементов, составляющих основную подгруппу и имеющих валентность, равную или близкую номеру группы. [17]

Этим вызывается отмеченная выше вторичная периодичность в изменении свойств атомов с изменением зарядов их ядер и факты провала электрона. [18]

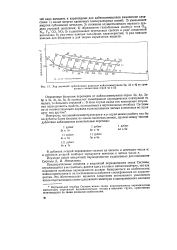Ход значений орбитальных радиусов кайносимметриков 2р, 3d и 4 / j по срав. [19]

Предварительные сведения о вторичной периодичности строк Системы, отражающейся в ее столбцах, даются здесь в главе о кайносимметрии, так как понимание проблемы периодичности должно базироваться на особенностях кайносимметриков и на постепенном ослаблении специфических их характеристик. [20]

До сих пор вторичную периодичность отмечали главным образом для элементов главных подгрупп; рис. 62 свидетельствует о том, что она существует для s - электронов и в дополнительных подгруппах. Интересно, отметить, что Zn, Cd, Hg, а также Си, Ag, Аи, имеющие наибольшие значения суммы ( / I / и), а также наименьшие радиусы атомов и ионов среди многочисленных металлов Системы, отличаются заметными ядовитыми свойствами в отношении живых клеток. [21]

Наряду с упомянутой выше вторичной периодичностью, являющейся следствием d - и / - сжатия и появления кайносимметричных 2р - и 3 / - орбиталей у первых представителей тип-аналогов, в Периодической системе элементов существует еще один вид периодичности в горизонтальных рядах р -, d - и / - элементов. Это так называемая внутренняя периодичность, сущность которой состоит в немонотонном изменении в этих рядах характеристик атомов, отражающих устойчивость заполняющихся валентных электронных орбиталей. Таким образом, шесть р-элементов отчетливо разделяются на две тройки. [22]

Наряду с упомянутой выше вторичной периодичностью, являющейся следствием d - и / - сжатия и появления кайносимметричных 2 / 7 - и Sd-орбиталей у первых представителей тип-аналогов, в системе элементов Д. И. Менделеева существует еще один тип периодичности в горизонтальных рядах р, d - и / - элементов. Это так называемая внутренняя периодичность, сущность которой состоит в немонотонном изменении в этих рядах характеристик атомов, отражающих устойчивость заполняющихся валентных электронных ор-биталей. [23]

Наряду с упомянутой выше вторичной периодичностью, являющейся следствием d - и / сжатия и появления кайносимметричных С2р - и 3 / - орбиталей у первых представителей тип-аналогов, в Периодической системе элементов существует еще один вид периодичности в горизонтальных рядах р -, d - и / - элементов. Это так называемая внутренняя периодичность, сущность которой состоит в немонотонном изменении в этих рядах характеристик атомов, отражающих устойчивость заполняющихся валентных электронных орбиталей. [24]

В чем заключается явление вторичной периодичности, наблюдаемое у галогенов. [25]

Центральное положение фосфора и его энергетическая характеристика по. [26]

В столбце N-Bi ярко выражена вторичная периодичность. [27]

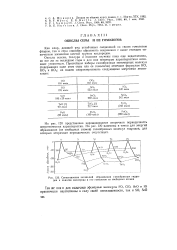Сопоставление энтальпий образования газообразных гидридов и окислов кислорода и его гомологов из свободных атомов. [28]

На рис. 120 представлена зарождающаяся вторичная периодичность энергетических характеристик. На рис. 120 нанесены и точки для энергий образования ( из свободных атомов) газообразных молекул гидридов, для которых вторичная периодичность отсутствует. [29]

Щелочные и щелочноземельные металлы также проявляют вторичную периодичность радиусов. [30]

Страницы: 1 2 3 4 5