Пернелла

Cтраница 2

Бохемен и Пернелл [323] объяснили это влиянием члена, содержащего теплоемкость, в общем выражении для потери тепла. [16]

Бохемен и Пернелл высказали предположение, что диффузия за счет многообразия возможных путей возникает вследствие различия скоростей при прохождении через каналы различных поперечных сечений. [17]

Бохемен и Пернелл [4] показали, что для данной нити, как предсказывалось, чувствительность возрастает с увеличением гс. Увеличение диаметра ячейки от 1 25 до 3 5 мм приблизительно удваивает температуру нити и, следовательно, чувствительность. [18]

Хор и Пернелл [16] показали, что график зависимости логарифма удерживаемого объема, измеренного при нескольких температурах колонки, от логарифма упругости пара растворенного вещества при этих температурах является линейным и имеет угловой коэффициент а, равный отношению теплоты растворения к теплоте испарения. [19]

Интерес представляют также доклад Пернелла и Квинна по теории экспрессной хроматографии, работы Скотта и Дести с сотрудниками по капиллярной хроматографии, Хюйтена и др. по теории препаративной хроматографии и многочисленные доклады по применению хроматографии для решения разнообразных вопросов. [21]

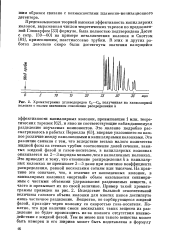Хроматограмма углеводородов С5 - Св, полученная на капиллярной колонке с малым значением отношения распределения k. [23]

Это явление подробно рассматривалось в работах Пернелла [63], впервые указавшего на важное различие между наполненными и капиллярными колонками. Это различие связано с тем, что вследствие весьма малого количества жидкой фазы на стенках трубки соотношение долей сечения, занятых жидкой фазой и газом-носителем, в капиллярных колонках оказывается на 2 - 3 порядка меньше чем в наполненных колонках. Это приводит к тому, что отношение распределения k в капиллярных колонках не превышает 3 - 5 даже при величине коэффициента распределения, равной нескольким сотням или тысячам. На практике это означает, что, в отличие от наполненных колонок, в капиллярных колонках мертвый объем оказывается соизмеримым с чистыми объемами удерживания разделяемых веществ, а часто и превышает их по своей величине. Вследствие большой относительной величины газового объема колонки для многих пиков достигнуто лишь частичное разделение. Вещество, не сорбирующееся жидкой фазой, проходит через колонку со скоростью газа-носителя. Понятно, что при наличии смеси нескольких таких веществ их разделение не будет происходить из-за полного отсутствия взаимодействия с жидкой фазой. [24]

Авторы трех предыдущих статей Скотт и Хейзлдин, Дести и Голдап, Пернелл и Квин, обсуждая метод высокоскоростной газовой хроматографии, исходили из допущения, которое, мне кажется, затемняет истинное положение вещей. Наиболее отчетливо оно сформулировано Дести и Голдапом на стр. [25]

В отношении интерпретации / Св метод Мартира - Ридла характеризуется теми же ограничениями, что и метод Кадогана - Пернелла. [26]

Так как в случае идеальной системы AHV / AHV 1, то неидеальность системы характеризуется положительными или отрицательными отклонениями. Хор и Пернелл ( 1956) по данным удерживания и по давлению пара этана и пропана при 21 определили таким способом, что давление пара бутана равно 1642 мм рт. ст.; эта величина хорошо согласуется с величиной, равной 1634 мм рт. ст., определенной другим способом. [27]

Из трех членов классического уравнения Ван-Деемтера член, учитывающий однородность набивки, оказался наиболее дискуссионным. Бохемен и Пернелл [3 ], работая с узкими фракциями силоцеля, и Литтлвуд [23], работая с однородными стеклянными шариками, как показывает табл. V-3, получили малые и даже отрицательные значения А. [28]

Из трех членов классического уравнения Ван-Деемтера член, учитывающий однородность набивки, оказался наиболее дискуссионным. Бохемен и Пернелл [3], работая с узкими фракциями силоцеля, и Литтлвуд [23], работая с однородными стеклянными шариками, как показывает табл. V-3, получили малые и даже отрицательные значения А. [29]

Эти результаты представляются особенно поразительными, если вспомнить, что для насадочных колонок рассчитанное число теоретических тарелок возрастает с увеличением удерживаемого объема. Не менее поразителен и тот факт, что при определенных условиях существует незначительное различие в действительной разделяющей способности капиллярной колонки и эффективной насадочной колонки, несмотря на то, что расчетные кажущиеся ( выраженные в теоретических тарелках) эффективности этих двух колонок могут различаться в 100 раз. Пернелл [19], например, показал, что капиллярная колонка с эффективностью 500 000 теоретических тарелок дает практически такое же разделение углеводородов, как и 2 5-метровая насадочная колонка с эффективностью 5000 теоретических тарелок. [30]

Страницы: 1 2 3