Плотность - замедление
Cтраница 2
Вторая поправка является попыткой учесть ошибку использования плотности замедления при вычислении г2 вместо нейтронного потока и сводится к получению более точной формулы, зависящей от нейтронного потока. [16]
Последнее соотношение вытекает из того факта, что плотность замедления пропорциональна потоку быстрых нейтронов [ см. уравнение (6.6), связывающее эти величины ], а мы требуем, как обычно, чтобы поток нейтронов всех энергий удовлетворял нулевому условию на экстраполированной границе. [17]
Мы можем оценить ошибку в эксперименте, в котором определяется плотность замедления вблизи точечного источника, если только мы знаем размеры призмы, с помощью которой этот эксперимент производился. [18]
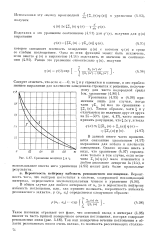 |
Сравнение величин и. [19] |
В данной книге часто применяются связанные уравнением (4.97) выражения для потока и плотности замедления. [20]
Если общие массы горючего и замедлителя в обеих системах одинаковы, то объемно-весовая плотность замедления т ] 2р также одинакова в обеих системах. [21]
Все нейтроны, генерируемые источниками с летаргией, меньшей и, дают вклад в плотность замедления для летаргии и. Общий вклад всех источников вычисляется интегрированием выражения (6.44) по всему интервалу летаргии ( 0, и) и по всей области пространства, где есть источники. Если, например, S ( г0, и0) дает реакция деления в реакторе, то и. [22]
Эта трудность обусловлена тем, что миграция нейтронов в процессе замедления и пространственная зависимость плотности замедления иные, чем при делении на тепловых нейтронах. Кроме того, здесь, очевидно, появляется дополнительный источник тепловых нейтронов из отражателя, так как некоторая часть нейтронов замедляется в нем. [23]
Действительно, допущение (8.370) - только одно из многих возможных способов задания соотношения между плотностью замедления и потоками. [24]
Заметим, что интегральное условие ( 3) непосредственно вытекает из предположения, что Q - плотность замедления в среде без поглощения. [25]
Полученное соотношение является условием критичности для бесконечного гомогенного реактора, в котором использовалось асимптотическое решение для плотности замедления и понятие тепловой группы. [26]
Для фактического выполнения расчетов на базе уравнений (8.391), кроме выбора распределения источников, необходимо выбрать соотношение между плотностью замедления при значениях летаргии, соответствующих границам группы, и усредненным потоком или усредненной плотностью замедления в группе. [27]
В выражение (6.47) вместо 2S входит S, вследствие тех предположений, которые были сделаны в (6.6) о соотношении между плотностью замедления и потоком. Так что в большинстве случаев, когда можно ожидать, что эта теория даст хорошие результаты, оба выражения для т дают примерно одинаковый результат. [28]
Другая аналогия, представляющая некоторый интерес, состоит в том, что скорость реакции R имеет те же математические свойства, что и функция плотности замедления q ( г, т), которая вводится в гл. Брейта - Вигнера ( см. § 6.5), который имеет большое практическое значение для управления реактором. [29]
Мы решим эту задачу методом ложных источников. Возьмем решение для плотности замедления в бесконечной среде от плоского источника и, составив систему чередующихся источников вне пластины, добьемся, чтобы поток на экстраполированной границе обращался в нуль, как того требуют граничные условия. [30]
Страницы: 1 2 3 4