Плотность - нормальное распределение
Cтраница 1
 |
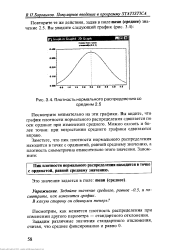
Плотность нормального распределения со средним 1. [1] |
Плотность нормального распределения симметрична относительно среднего. Среднее значение определяет меру расположения плотности. Среднее значение нормального распределения совпадает с медианой и модой. [2]
Плотность нормального распределения можно задать также через элементы обратной матрицы К-1 таким образом, как это сделано в определении 10.11 при рассмотрении двумерной СВ. [3]
 |
Плотность нормального распределения со средним. [4] |
Пик плотности нормального распределения находится в точке с ординатой, равной среднему значению. [5]
Так как плотность нормального распределения отлична от нуля в интервале ( - оо, оо), то среднее значение ц должно быть существенно больше нуля и ( я - Зст) должно быть также положительно, если для положительного аргумента X вместо усеченного нормального распределения приближенно использовать нормальное распределение. [6]
Так как плотность нормального распределения отлична от нуля в интервале ( - оо. За) должно быть также положительно, если для положительного аргумента X вместо усеченного нормального распределения приближенно использовать нормальное распределение. [7]
Использование функции плотности нормального распределения позволяет вычислить частоту ( вероятность) появления случайной величины. [8]
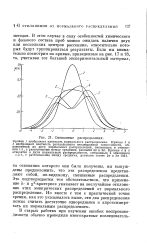 |
Смешанные распределения. [9] |
Кривая 1 изображает плотность нормального распределения. [10]
Они напоминают по форме плотность нормального распределения, но при t - - со значительно медленнее сближаются с осью абсцисс. При / - - оо дисперсия 2 - кг2, поэтому распределение Стью-дента сближается с нормальным; случай / оо вообще соответствует нормальному распределению. При малых же / распределениеСтьюдента сильно отличается от нормального, в силу чего его роль особенно велика в так называемой микростатистике или статистике малых выборок. [11]
Заметьте, что пик плотности нормального распределения находится в точке с ординатой, равной среднему значению, а плотность симметрична относительно этого значения. [12]
Итак, при увеличении дисперсии плотность нормального распределения расплывается или рассеивается относительно среднего значения, при уменьшении дисперсии она, наоборот, сжимается, концентрируясь возле одной точки - точки максимального значения. [13]
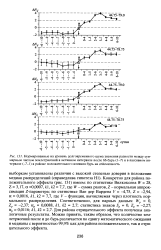
На рис. 167 приводится график плотности нормального распределения X с нанесенными на нем значениями указанных величин. [14]
Страницы: 1 2 3 4