Плотность - нормальное распределение
Cтраница 2
V - функция, вычисляемая через плотность нормального распределения. Для района отрицательного эффекта получены аналогичные результаты. Можно принять, таким образом, что количество землетрясений после и до бурь различается по сдвигу математического ожидания и медианы с вероятностью 99 9 % как для района положительного, так и отрицательного эффекта. [16]
Наименее благоприятная ПРВ этой модели равна плотности нормального распределения. Поэтому оптимальные для гауссова шума алгоритмы являются по существу асимптотически ро-бастными алгоритмами для широкого класса распределений. Именно этим фактом и объясняется успешное применение оптимальных для гауссова шума алгоритмов в тех случаях, когда отсутствуют достаточные основания для представления шума гауссовым процессом. [17]
График на рис. 18 - 3 иллюстрирует вид плотности нормального распределения. [18]
 |
Функция плотности распределения Пуассона для ХГ2 5. [19] |
Функция Ф ( х) является нормированной функцией плотности нормального распределения. [20]
 |
Функция [ IMAGE ] Плотность.| Функция нормального [ IMAGE ] Плотность нормального. [21] |
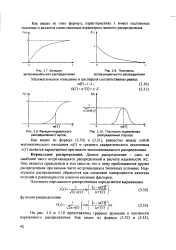
На рис. 3.9 и 3.10 представлены графики функции и плотности нормального распределения. [22]
Результаты сравнения плотности распределений Эрланга, статистической плотности и плотности нормального распределения приведены на рис. 7.5. Так же, как и проверка по критерию Пирсона, они свидетельствуют в пользу распределений Эрланга. [23]
В этом случае, как видно из (3.27), величина Р описывается плотностью нормального распределения вероятностей. Это означает, что все топливо, проникшее в бедную часть факела, сгореть не может. Знак величины v в этом случае также играет важнейшую роль. X z скорость среды относительно поверхности z Zj всегда направлена в бедную часть факела, т.е. несгоревшее топливо конвективными движениями оттесняется от зоны реакции. [24]
Здесь ставится вопрос о том, когда плотности распределения нормированных сумм сходятся к плотности нормального распределения, если соответственные функции распределения сходятся к нормальной. Этот вопрос получает исчерпывающее решение в следующей теореме. [25]
Здесь ставится вопрос о том, когда плотности распределения нормированных сумм сходятся к плотности нормального распределения, если соответствующие функции распределения сходятся к нормальной. [26]
Для отыскания приближенного решения примем, что оно имеет вид эквивалентный выражению для плотности нормального распределения вероятности. [27]
В подавляющем большинстве случаев для эмпирического распределения можно получить хорошее аналитическое приближение, если использовать плотность стандартного нормального распределения р ( х) и некоторые ее производные. [28]
Плотность распределения Коши имеет вид симметричной относительно точки х а кривой, визуально очень похожей на плотность нормального распределения. [29]
Оказывается, если от точки среднего, или, что тоже самое, от точки максимума плотности нормального распределения отложить вправо и влево соответственно два и три стандартных отклонения ( 2 и 3 сигма), то площадь под графиком нормальной плотности, подсчитанная по этому промежутку, будет соответственно равна 95.45 % и 99.73 % всей площади под графиком. [30]
Страницы: 1 2 3 4