Зарядовая плотность
Cтраница 2
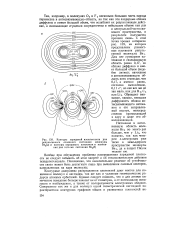 |
Контуры зарядовой изоплотности для репульсивного основного состояния молекулы Ве2 ( а и контуры зарядового натекания и вытекания для того же состояния Ве2 ( б. [16] |
Вообще при обсуждении проблемы распределения зарядовой плотности не следует забывать об этом запрете и об отталкивательном действии псевдопотенциала. Несомненно, что окончательное решение об устойчивости связи может быть достигнуто лишь при вычислении силовых векторов, направленных на ядра молекулы. [17]
Однако выполненные затем расчеты [7, 8] волны зарядовой плотности по методу Хартри - Фока не дали повода чем-то выделить степень заполнения 1 / 3, хотя и привели к энергии конденсации порядка ez / l на частицу. Теория Хартри - Фока относится к разряду методов среднего поля со всеми их трудностями в двумерных задачах и с возможностью упустить важные физические факторы. Однако трудность в получении энергии соразмерной конфигурации из хартри-фоковского основного состояния является достаточно серьезной проблемой, вызывающей сомнения в справедливости гипотезы о волне зарядовой плотности. [18]
Интегрирование ведется по всему пространству изменения зарядовой плотности р ( г) и угла f между радиусом-вектором г и осью симметрии. [19]
На рис. 107 видны области натекания зарядовой плотности и области ее вытекания. При переходе от основного состояния молекулы Oz - X32g к состояниям aAff и 642g рис. 107 меняется следующим образом. Оказывается, что добавочные натяжения и вытекания плотности при сравнении возбужденных и основного молекулярного состояния ничтожны - они меньше 0 1 % от значений общей зарядовой плотности в любой из точек пространства, а контуры с плотностью 0 002 е - накладываются друг на друга: и это несмотря на вполне заметные энергетические скачки, сопровождающие возбуждения. [20]
Интегрирование ведется по всему пространству изменения зарядовой плотности р ( г) и угла j между радиусом-вектором г и осью симметрии. [21]
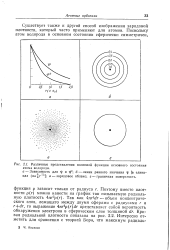 |
Различные представления волновой функции основного состояния атома водорода. а - Зависимость для ty и ф2. б - линии равного значения t [ в едини. [22] |
Существует также и другой способ изображения зарядовой плотности, который часто применяют для атомов. [23]
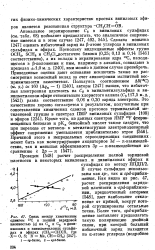 |
Связь между химическим. [24] |
Как видно из рис. 47, расчет распределения зарядовой плотности в - spd - приближе-нид, предпочтенный авторами [548], дает наибольшее отклонение от прямой, вокруг которой сгруппированы остальные точки. [25]
Как видно из рис. 47, расчет распределения зарядовой плотности в - spd - приближе-щаи, предпочтенный авторами [548], дает наибольшее отклонение вт прямой, вокруг которой сгруппированы остальные точки. Более того, spd - прибли-жение заставляет предполагать такую. [27]
 |
Нормальные моды динамики плазмы. [28] |
Флуктуации электронной плотности v приводят к локальному отклонению зарядовой плотности от равновесной ( ибо положительный фон все время остается однородным); таким образом, появляется локальный объемный заряд. В результате электростатического взаимодействия между электронами и фоном возникает возвращающая сила, которая стремится восстановить равновесное распределение электронов. Однако электроны обладают кинетической энергией и поэтому проскакивают мимо своего равновесного положения, так что процесс начинается снова, но идет уже в противоположном направлении. [29]
Если решить уравнение Лапласа для задачи о флуктуациях зарядовой плотности в полубесконечном электронном газе, резко обрывающемся на плоской поверхности, то решениями будут плазменные колебания, которые будут периодичны в плоскости поверхности, но экспоненциально спадать внутрь электронного газа ( см. напр. Квант этих колебаний называется поверхностным плазмо-ном. [30]
Страницы: 1 2 3 4 5
