Спектральная плотность - мощность
Cтраница 1
Спектральная плотность мощности на входе, в отличие от спектральной плотности квадрата напряжения, представляет собой преобразование Фурье для функции взаимной корреляции между напряжением и током. [1]
Спектральная плотность мощности на выходе преобразователя определяется взаимной мощностью между моментом и скоростью. Она равна отношению квадрата спектральной плотности момента к адмитансу. [2]
Спектральная плотность мощности С7 ( ш) позволяет судить о частотных свойствах случайного процесса 1 ( 0 - Она характеризует его интенсивность при различных частотах со или, иначе, среднюю мощность, приходящуюся на единицу полосы. [3]
Спектральная плотность мощности может быть определена также и следующим образом. Фурье (3.16), считая, что вне интервала при t Т реализация равна нулю. [4]
Спектральная плотность мощности может рассматриваться как плотность вероятности присутствия в случайном процессе колебаний с теми или иными частотами. [5]
Спектральная плотность мощности, соответствующая автокорреляционной функции, является действительной неотрицательной функцией частоты и четной функцией со. [6]
Спектральная плотность мощности Ф ( со), соответствующая автокорреляционной функции, сохраняет информацию, которая содержится в амплитудном спектре сигнала, но опускает всякую информацию, относящуюся к фазе. Так как фазовая информация существенна при определении формы функции во временной области, то Ф [ [ ( со) может соответствовать многим различным множествам случайных функций. Спектральная плотность мощности Ф ( со), соответствующая взаимной корреляционной функции, необязательно является действительной функцией и поэтому сохраняет некоторую информацию о фазе, содержащуюся в случайных сигналах. [7]
Спектральная плотность мощности ( отнесенная к g2) при динамических перемещениях конструкции самолета в месте расположения антенны, определенная для случая стрельбы из пушек, составляла примерно 2 Гц в окрестности основной резонансной частоты антенны, равной 485 Гц. Столь значительная вибрация, усиленная резонансными колебаниями антенны, привела к возникновению очень больших. [8]
Спектральная плотность мощности G ( co) характеризует интенсивность случайного процесса x ( t) при различных частотах со. Она определяет среднюю мощность, приходящуюся на единицу полосы частот. Величина G ( co) может быть определена прямым и косвенным методом. [9]
Спектральная плотность мощности дискретной последовательности имеет множителем величину 1 / 7 определяющую изменение размерности и масштаба относительно функции Sx ( f), это изменение, свойственное и другим характеристикам процесса x ( t), связано, очевидно, с выбором в качестве процесса - переносчика функции отсчетов в виде периодической последовательности дельта-функций. [10]
Спектральную плотность мощности определяют с помощью устройств, называемых анализаторами спектра или спектроанализаторами. Оценки спектральной плотности мощности эргодического стационарного случайного процесса получают одним из трех методов. [11]
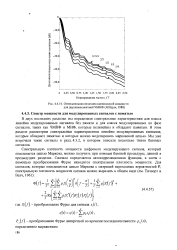 |
Относительная величина внеполосной мощности для двухкомпонентной ЧМНФ ( Milligan, 1988. [12] |
Спектральную плотность мощности цифрового модулирующего сигнала, который описывается цепью Маркова, можно получить при помощи базовой процедуры, данной в предыдущих разделах. Сначала определяется автокорреляционная функция, а затем с помощью преобразования Фурье находится спектральная плотность мощности. [13]
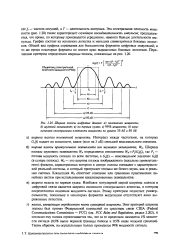 |
Ширина полосы цифровых данных. а половинная мощность. 6 шумовой эквивалент. в по первым нулям. г 99 % мощности. д ограниченная спектральная плотность мощности по уровню 35 дБ и 50 дБ. [14] |
Эта спектральная плотность мощности ( рис. 1.20) также характеризует случайную последовательность импульсов; предполагается, что время, по которому производится усреднение, намного больше длительности импульса. График состоит из основного лепестка и меньших симметричных боковых лепестков. Общий вид графика справедлив для большинства форматов цифровых модуляций; в то же время некоторые форматы не имеют ярко выраженных боковых лепестков. [15]
Страницы: 1 2 3 4