Характеристическая поверхность

Cтраница 4

В теории течения газов фундаментальную роль играют характеристические поверхности соответствующих уравнений, смысл которых заключен в следующем. [46]

Как мы уже отмечали [138], на характеристической поверхности имеются соотношения между функцией и, удовлетворяющей уравнению ( 167), и ее производными. [47]

В случае плоского стационарного течения газа вместо характеристических поверхностей можно говорить о характеристических линиях ( или просто характеристиках) в плоскости движения. Через всякую точку О этой плоскости проходят две характеристики ( ААГ и В В1 на рис. 51), пересекающие проходящую через эту же точку линию тока под углами, равными углу Маха. Ветви О А и О В характеристик, направленные вниз по течению, можно назвать исходящими из точки О; они ограничивают область АОВ течения, на которую могут влиять исходящие из точки О возмущения. [48]

Из предыдущего исследования известно, что для такой характеристической поверхности задачу Коши вообще разрешить нельзя. В линейном случае, когда коэффициенты а ы и Ь в уравнениях (48.5) зависят только от xt и не зависят от uk, характеристические поверхности определяются для данной системы раз и навсегда. В более общем случае, который имеет место в теории пластичности ( а также и в газовой динамике), особый характер поверхности зависит от самой поверхности 5 и от заданных на ней величин. Уравнение (51.5) называется характеристическим условием или условием направления. [49]

В общем случае им соответствуют еще два семейства характеристических поверхностей, касающихся в каждой своей точке одного из этих направлений. [50]

При этом согласно полученным результатам возможны три варианта характеристической поверхности тензора проницаемости - сфера для изотропных величин проницаемости, эллипсоид вращения при равенстве проницаемости по двум главным направлениям и трехосный эллипсоид при различных значениях проницаемости по трем главным направлениям. [51]

Тогда поверхность uj ( x ] 0 называется характеристической поверхностью ( или характеристикой) квазилинейного дифференциального уравнения ( 1), а уравнение ( 16) - характеристическим уравнением. При п 2 характеристическая поверхность называется характеристической линией. [52]

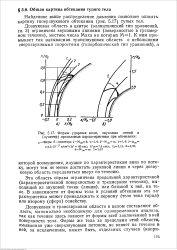Формы ударных волн, звуковых линий и ( пунктир лределыные характеристики при обтекадии. [53]

Эта область справа ограничена предельной характеристикой, ( характеристической поверхностью в трехмерном течении), выходящей из звуковой точки ( линии), или близкой к ней, на теле. В зависимости от формы тела и условий обтекания эта характеристика может принадлежать к первому ( тело типа торца) или второму ( сфера) семейству. [54]

Страницы: 1 2 3 4