Электронная подсистема
Cтраница 1
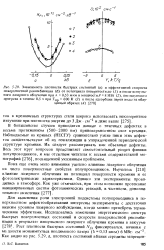
Электронная подсистема осуществляет формирование электрических управляющих и питающих напряжений, а также преобразование выходного корреляционного поля в электрический сигнал с целью его визуализации и дальнейшей обработки для автоматического определения координат корреляционного максимума. [1]
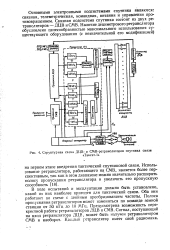 |
Структурная схема ДЦВ - и СМВ-ретрансляторов спутника связи. [2] |
Основными электронными подсистемами спутника являются: связная, телеметрическая, командная, питания и управления про-тивовращением. Связная подсистема спутника состоит из двух ретрансляторов - ДЦВ и СМВ. [3]
С электронной подсистемой связано поглощение при внутризонных переходах в полупроводниках, проявляющихся в виде широких слабоструктуриров. [4]
Динамическое описание электронной подсистемы удобно вести на языке характерных длин. Не считая боровского радиуса ао, имеются четыре такие длины. [5]
Волновую функцию электронной подсистемы Ф ( г К) находят из уравнения (2.10), которое можно толковать как уравнение Шредингера для электронной подсистемы в поле неподвижных ядер. Энергия W ( R) электронной подсистемы является функцией координат ядер, ее принято называть адиабатическим потенциалом. Она играет роль добавочной потенциальной энергии в уравнении (2.11) для ядерной подсистемы. [6]
 |
Модели M ( F2 - и R ( F3 - центров в ЩГК ( е - - анионная вакансия, захватившая электрон.| Модели N-центров. [7] |
При возбуждении электронной подсистемы дефекта происходит существенная перестройка окружения, так что симметрия системы в целом изменяется. В теории кристаллов с точечными дефектами обычно ввиду трудности рассматриваемой задачи сначала проводят расчет без учета искажения кристаллической решетки дефектом, а затем уже оценивают это искажение с помощью полученных приближенных волновых функций. Поэтому симметрию данной системы на первом этапе определяют исходя из рассмотренных выше соображений. [8]
Большое значение учета электронной подсистемы видно уже при использовании простейшей модели свободных электронов. Рассмотрим для примера в рамках этой модели образование вакансии в одновалентном металле. [9]
Последовательное квантовомеханическое рассмотрение электронной подсистемы молекулы, а тем более кристалла, является чрезвычайно сложной задачей и практически осуществимо лишь на основе приближенных методов. [10]
Для выяснения роли электронной подсистемы полупроводника в поверхностном дефектообразовании интересны эксперименты с достаточно низким уровнем лазерного возбуждения, когда можно пренебречь термическими эффектами. [12]
Оператор числа частиц для электронной подсистемы Ne включен в набор базисных переменных, так как предполагается использование большого ансамбля, наиболее подходящего для рассматриваемой задачи. Отметим также, что энергия взаимодействия Я включена в гамильтониан термостата. [13]
Таким образом, изменение энергии электронной подсистемы дает значительный вклад в энергию образования точечных дефектов в металлах. [14]
Наряду с переходами между уровнями в электронной подсистеме всего кристалла, в спектрах - кристаллов проявляются переходы между локальными уровнями дефектов кристаллич. Дефекты образуют в кристаллах центры поглощения ( центры окраски) и центры люминесценции. Примером простейшего центра окраски в щелочно-галоидных кристаллах являются / - центры, представляющие собой анионную вакансию, захватившую электрон. Система уровней такого центра аналогична системе уровней атома водорода, только смещенной в ДВ-область и уширенной вследствие взаимодействия с колебаниями атомов кристаллич. [15]
Страницы: 1 2 3 4