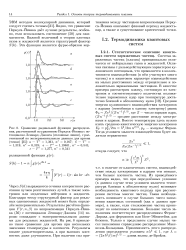
Квантовый подход
Cтраница 2
Таким образом, предлагаемая логика автоматически приводит к классической цепи Маркова, а квантовый подход понадобился лишь для нахождения вероятностей перехода от одного измерения к другому. [16]
Однако оказывается, что если число фотонов в данной моде резонатора намного превышает единицу, то ( усредненные) результаты квантового подхода совпадают с результатами полуклассической теории. [17]
Из приведенного примера видно, что при определенных условиях ( в данном случае этим условием является температура близкая к абсолютному нулю) возникает необходимость квантового подхода при рассмотрении системы многих частиц. Такая необходимость возникает в случае больших чисел заполнения квантовых состояний ( как в данном примере), а также, если столкновение частиц происходит по квантовым законам. Большие числа заполнения соответствуют распределениям Ферми-Дирака для фермионов или Бозе-Эйнштейна для бозонов. Только в предельном случае малых чисел заполнения справедливо распределение Макс-велла - Больцмана. [19]
Подход Шнайдера был основан на квантово-механических представлениях, подход Гапонова-Грехова был классическим. Квантовый подход [13] основан на том, что электрон, вращающийся в однородном магнитном поле, ведет себя как ангармонический осциллятор, энергетический спектр которого неэквидистантный. На частотах, близких к HOJQ, осциллятор подобен трехуровневой квантовой системе: он поглощает энергию на частоте перехода и п р р и излучает - на и р п-р. [20]
При квантовом подходе этот процесс интерпретируется следующим образом. Дополнительное осциллирующее магнитное поле эквивалентно наличию квантов электромагнитного излучения Лео, где со - частота осциллирующего поля. [21]
При полуклассическом подходе считалось, что ц является оператором, а Е - классической величиной. При полностью квантовом подходе обе величины являются операторами. [22]
Применим ли квантовый подход к явлениям интерференции света, проявляющейся, например, в опыте Юнга. [23]
Первый раздел этой работы будет посвящен рассмотрению задачи резонансного воздействия внешнего поля в приближении линейного отклика, т.е. линейной зависимости поляризации системы от величины лазерного поля. На основе квантового подхода будут получены уравнения для дипольного момента частиц с учетом внешнего и самосогласованного поля, действующих на данную частицу. Будут получены формулы для резонансного усиления поля с учетом статистики фрактала. [24]
Для рассеяния света на электронах вещества условие связанности электронов не является обязательным, рассеяние света может происходить и на свободных электронах. Комптон впервые показал, что квантовый подход к задаче рассеяния рентгеновских лучей на почти свободных электронах легких веществ приводит к результатам, существенно отличающимся от классических. [25]
Для рассеяния света на электронах вещества условие связанности электронов не является обязательным, рассеяние света может происходить и на свободных электронах. Комптон впервые показал, что квантовый подход к задаче рассеяния рентгеновских лучей на почти свободных электронах легких ве-ществ приводит к результатам, существенно отличающимся от классических. [26]
Требование удовлетворения принципу соответствия отнюдь не является тривиальным. Возникает вопрос, как согласовать квантовый подход, основанный на рассмотрении вероятностей, с классическим, допускающим точное предсказание поведения системы. Рассмотрим с этой точки зрения уже разобранный выше пример рассеяния фотонов свободными электронами. Как видно из формулы (1.11), максимально возможное увеличение длины волны при единичном акте рассеяния фотона равно 2 / i / ( m0c), что примерно составляет 10 - 10 см. Это слишком маленькая величина, чтобы ее можно было заметить при рассеянии радиоволн с длиной волны порядка 1 см и больше. Легко подсчитать, какую наибольшую энергию может приобрести электрон в результате рассеяния одного такого фотона. С помощью формулы (1.10) находим, что A. Для того чтобы в результате рассеяния радиоволн приобрести энергию всего в 1 зВ, электрон должен рассеять по меньшей мере 1014 квантов. [27]
Для рассеяния света на электронах вещества условие связанности электронов не является обязательным, рассеяние света может происходить и на свободных электронах. Комптон впервые показал, что квантовый подход к задаче рассеяния рентгеновских лучей на почти свободных электронах легких веществ приводит к результатам, существенно отличающимся от классических. [28]
В 1.2.1 мы уже касались условий, при которых возникает необходимость квантового подхода при рассмотрении системы многих частиц. Здесь нас будет интересовать система заряженных частиц ( плазма), находящаяся в равновесии при некоторой конечной температуре. [29]
Полуклассический подход, вообще говоря, был полностью справедлив для рассматриваемых задач. Однако в задачах, в которых учитываются спонтанное излучение и шумы, необходимо применять полностью квантовый подход, при котором как поле, так и среда квантуются. [30]
Страницы: 1 2 3