Численный подход
Cтраница 1
 |
Распространение профиля плотности для граничного условия ( II. k / h 0, 5 ( a. k / h 0, 05 ( 6. hj i / hj 1, 05 ( с. [1] |
Численный подход позволяет сконструировать граничное условие, специально приспособленное для поглощения высокочастотных волн. [2]
Численный подход упрощает проверку условий, задаваемых неравенствами. Если для какого-либо узла сетки наложенное ограничение не выполняется, то этот узел не рассматривается. Проверяются смежные узлы, пока они еще не выходят за пределы допустимой области. При увеличении числа ограничений уменьшается допустимая область, но это не затрудняет вычисления. В противоположность этому решение задач с помощью точных аналитических методов с ростом числа ограничений усложняется. [3]
В работе развивается численный подход [1-3] к исследованию напряженного состояния ( НС) в осесимметричных узлах ввода плоских крышек в зависимости от диаметров крышки и ввода, толщин их стенок и радиуса наружной галтели, сопрягающей поверхность крышки и патрубка. Напряженное состояние в этих местах является объемным [1], что приводит к необходимости расчетного моделирования искомого НС на основе уравнений теории упругости. Развитие методов и средств вычислений, прежде всего метода конечных элементов ( МКЭ), позволяет автоматизировать проведение таких исследований. Результаты исследования НС более 400 конструктивных вариантов представлены в виде графических зависимостей, позволяющих выявить особенности исследуемого НС и зависимость уровня концентрации напряжений от радиуса гантельного перехода и других геометрических параметров в широком диапазоне их изменения. [4]
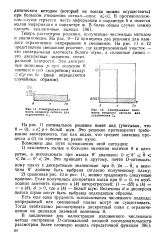 |
Спектральная плотность входного сигнала для ограничения С.| Спектральная плот-кость входного сигнала для ограничения С. [5] |
Есть еще одна трудность использования численного подхода: непрерывный или смешанный планы могут не существовать. [6]
При решении нелинейных износоконтактных задач широко используются численные подходы. Одним из наиболее широко используемых является пошаговый метод, в основе которого лежит дискретизация времени и использование конечно-разностного представления дифференциального или интегрального оператора. [7]
При решении нелинейных износоконтактных задач широко используются численные подходы как основанные на традиционных методах, так и использующие специфические процедуры. [8]
При решении нелинейных износоконтактных задач широко используются численные подходы. Одним из наиболее широко используемых является пошаговый метод, в основе которого лежит дискретизация времени и использование конечно-разностного представления дифференциального или интегрального оператора. [9]
Для; построения касательной матрицы жесткости применяют численный подход, который заключается в том, что концевые точки нити получают последовательно малые смещения вдоль координатных осей, для которых вычисляются концевые реакции. [10]
Это сходно с ранним примером и иллюстрирует гибкость численного подхода в возможности справиться с опционами, отличными от самых простых и элементарных. [11]
Почему для решения современных задач естествознания необходимо единство аналитического и численного подхода. [12]
В этом случае погрешность решений оказывается ниже, чем при традиционных численных подходах. [13]
Обтеканию пластинок вязкой жидкостью посвящены многочисленные исследования, основанные на асимптотических и численных подходах. Представление течения в окрестности носика пластинки в приближении Стокса и при малых числах Рейнольдса получено Карьером и Лином [33] в виде отрезка ряда с произвольными коэффициентами, отвечающими внешним граничным условиям. [14]
Сейчас всеми признано, что методы граничных и конечных элементов не следует рассматривать как конкурирующие численные подходы; ими следует пользоваться таким образом, чтобы извлечь пользу из специфических достоинств каждого из них. [15]
Страницы: 1 2 3