Геометрический подход

Cтраница 1

Геометрический подход к проблеме главных осей подчеркивает ту сторону теории, которая в чисто алгебраической трактовке не обнаруживается столь заметно. Когда мы рассматриваем матрицу в связи с поверхностью второго порядка, мы сразу видим, каков геометрический смысл главных осей. Но, кроме того, мы непосредственно усматриваем возможность изменения нашей системы координат. Так как главные оси взаимно ортогональны и имеют длину 1, то они представляются нам как естественная система координат, соответствующая заданной матрице. Поэтому целесообразно изучить теперь вопрос о преобразовании координат. [1]

Геометрический подход позволяет проводить рассмотрение глобально, что важно при изучении топологических свойств теории. [2]

Геометрический подход в опознавании образов основывается на гипотезе о компактности образов, гласящей, что в признаковом многомерном пространстве ( где каждая координата - признак - известное свойство соединения, выраженное в виде числа) реализации, относящиеся к одному образу, достаточно четко отделены от реализаций, относящихся к другим образам. [3]

Геометрический подход позволяет с гораздо более широких позиций взглянуть на фундаментальные проблемы теории управления: управляемость, наблюдаемость, инвариантность, декомпозицию и агрегирование. Особенно он полезен для исследования нелинейных систем управления, трудности анализа и синтеза которых общеизвестны. [4]

Геометрический подход к решению задачи оптимальной стабилизации для конечномерных систем, развитый в предыдущих главах, может быть распространен на системы, определенные в банаховом пространстве. В типичной ситуации характерной особенностью гамильтоновой системы, ассоциированной с общей абстрактной задачей оптимальной стабилизации, является свойство гиперболичности ее динамики в окрестности положения равновесия. Гиперболическая динамика хорошо изучена и позволяет восстанавливать сепаратрисные многообразия итеративно с любой степенью точности. [5]

Геометрические подходы к синтезу сигналов и детектированию, которые были представлены при рассмотрении цифровой модуляции, имеют свои корни в оригинальных работах Шеннона. [6]

Геометрический подход к оценке максимального правдоподобия для бесконечномерного гауссовского сдвига I, II, III / / Теория веро-ятн. [7]

Геометрический подход к исследованию клейновых групп опирается на понятие фундаментальной области. Фундаментальной областью разрывной группы Г называется множество FQ ( T), содержащее по одной точке жз каждой орбиты Fz0, z0 Q ( D, и такое, что каждая непустая его компонента F П Q - связна. Это множество не является открытым и, вообще говоря, не связно. [9]

Геометрический подход является наиболее простым и наглядным для понимания физической сущности явления. Поэтому на нем сконцентрируем основное внимание. Геометрический подход позволяет исследовать образование муаровых полос как результат пересечения двух систем линий: эталонной сетки и сетки, нанесенной на образец. Зная расстояние между линиями эталонной сетки и измерив расстояние между полосами, можно, прибегнув к геометрическому анализу пересечения двух систем линий, вычислить расстояние между линиями сетки образца в некотором участке и изменение их направления. Эти данные позволяют определить линейные и сдвиговые деформации. [10]

Геометрический подход к решению задач структурного анализа и синтеза линейных и инвариантных во времени многосвязных систем управления конечного динамического порядка, т.е. в предлагаемой теории рассматриваются системы функций с линейными законами преобразования. [11]

Геометрический подход к описанию структуры макромолекул позволяет вычислить с помощью методов, изложенных в гл. [12]

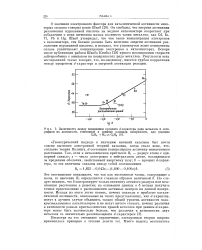Зависимость между изменением процента d - характера ряда металлов и логарифмом их активности, отнесенной к единице площади поверхности, для реакции. [13]

Геометрический подход к изучению явлений катализа был почти совсем вытеснен электронной теорией катализа, когда стало ясно, что, согласно теории Полинга, d - состояния контролируют величину межатомного расстояния. [14]

Страницы: 1 2 3 4