Закон - преобразование
Cтраница 1
Закон преобразования этих метрик при преобразовании координат х, у, z таков, что dSi и ds, остаются инвариантными. Одна метрика должна представлять как бы аналогию с измерением длин, а другая - с измерением углов геодезического поворота касательной вдоль кривых на какой-нибудь метрической поверхности. И, действительно, каждую поверхность можно снабдить парой метрик вида (4.9), которые будут играть именно эту роль. [1]
Закон преобразования (5.9) не является наиболее общим среди допускаемых супергруппой Вейля. В общем случае отношение L к L может быть произвольным в соответствии с отсутствием связи между дилатационным и киральным весами. Например, вариация R (5.2) содержит только параметр L. Один из способов рассмотрения таких вопросов включает решение кинематических связей и построение независимой связности с использованием комплексного скалярного поля if [4,8], которое фигурирует в решении. [2]
Закон преобразования (2.4) составляет содержание гдпо-тезы подобия, или масштабной инвариантности флуктуации. [3]
Закон преобразования компонент тензоров не зависит от их физической природы. Сначала рассмотрим образование простейших тензоров, установим законы преобразования их компонент и укажем общее определение тензора. [4]
Закон преобразования ковариантных компонент следует из инвариантности интервала относительно преобразований Лоренца. [5]
Закон преобразования их компонент таков, что новые компоненты являются линейными однородными многочленами от старых компонент. [6]
Закон преобразования определяется коэффициентами ац. [7]
Закон преобразования частоты легко получить путем преобразования фазового множителя волны. [8]
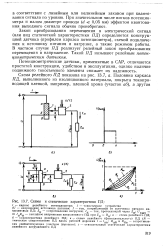 |
Схемы и статические характеристики ПД. [9] |
Закон преобразования перемещения в электрический сигнал ( или вид статической характеристики ПД) определяется конструкцией датчика ( профилем каркаса потенциометра), схемой подключения к источнику питания и нагрузке, а также режимом работы. В частном случае ПД реализует релейный закон преобразования перемещения в напряжение. Такой ПД называют релейным потенциометр ическим датчиком. [10]
Закон преобразования частоты легко получить путем преобразования фазового множителя волны. [11]
Закон преобразования Вигнера для векторов состояний (14.10), (14.11) может быть получен чисто математически при разыскании унитарных представлений группы Пуанкаре. Таков был подход самого Вигнера в его классической работе [7], и Вайнберг в работе [5] исходит непосредственно из этого результата. [12]
Закон преобразования разности между текущим и заданным значениями регулируемой величины в выходную ( регулирующую) величину представляет собой алгоритм функционирования автоматического регулятора. [13]
Закон преобразования характеристики какого-либо свойства при повороте осей координат ( и ранг соответствующего тензора) может быть выведен исходя из теоретических соображений. Сопоставление геометрического изображения этого закона в виде фигуры ( поверхности анизотропии) с экспериментальными данными может служить проверкой правильности исходных допущений, лежащих в основе вывода об их применимости к исследуемому материалу. [14]
Закон преобразования матрицы оператора получается из соотношения b С ( а), инвариантного относительно замен координат. [15]
Страницы: 1 2 3 4