Оптимальный закон - управление
Cтраница 2
Для реализации оптимального закона управления необходимо иметь представление о характере связи между переменными и о влиянии отдельных параметров на ход процесса производства бумаги. [16]
Задачу определения оптимального закона управления можно свести к нахождению множества точек переключения без построения оптимальных траекторий в пространстве состояний системы также и в случае, когда U является выпуклым ограниченным многогранником. [17]
Уравнения управления определяют оптимальный закон управления, например оптимальный план ( график или программу) работы предприятия. [18]
Положим, что заранее известен оптимальный закон управления как функция фазовых координат либо оптимальное управление как функция времени. [19]
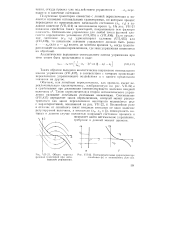 |
Общая картина фановых траекторий при оптимальном управлении. [20] |
Таким образом выведено аналитическое выражение оптимального закона управления ( VI 1 437), в соответствии с которым происходит переключение управляющего воздействия и с одного предельного значения на другое. [21]
Оптимальный закон управления (10.85) совпадает с оптимальным законом управления (9.74), (9.75) в детерминированном случае. Таким образом, случайное воздействие на объект и случайное начальное условие не влияют на оптимальный закон управления, если имеется полная информация о фазовом векторе. [22]
Оптимальный закон управления (10.89) совпадает с оптимальным законом управления (9.74), (9.75) в детерминированном случае и со стохастическим оптимальным управлением (10.85) при полной информации лишь с тем отличием, что в законе управления ( 10.89 а) используется не сам фазовый вектор, а его оценка, которая получается на выходе фильтра Калмана-Бьюси. [23]
Последнее выражение указывает на то, что искомый оптимальный закон управления характеризуется кусочно-постоянной функцией, имеющей предельные значения I и не более двух интервалов постоянного состояния. [24]
Основное отличие законов ( 12) от полученных ранее оптимальных законов управления ( 5) в том, что в построении движения участвуют все три обобщенные координаты. [25]
Убедитесь в том, что в зависимость, определяющую оптимальный закон управления, реализующий принцип обратной связи, входят слагаемые, вызванные наличием запаздываний по управлениям и состояниям. Отбрасывание членов, обусловленных запаздываниями, приводит к стандартной форме линейного квадратично-оптимального закона. [26]
Число базовых значений и1 вектора и, входящих в оптимальный закон управления, не превосходит ( k), где k - число ресурсных ограничений. [27]
 |
Блок-схемы адаптивных систем управления на базе нечеткого регулятора. [28] |
Я - вектор параметров нечеткого регулятора, который точно воспроизводит оптимальный закон управления. Согласно ( 7), сигнал управления нечеткого регулятора определяется как функция от переменных состояния. [29]
И если абсолютная разница функционалов меньше заданной величины, то поиск оптимального закона управления заканчивается. [30]
Страницы: 1 2 3 4