Полином - баттерворт
Cтраница 1
Полином Баттерворта обеспечивает максимально гладкое при - ближение к идеально прямоугольной частотно й характеристике фильтра нижних частот. При нулевой частоте значение функции Баттерворта и ее первых п - 1 производных точно совпадает с идеальной характеристикой, а далее разность значений непрерывно увеличивается, достигая максимума у границы полосы. [1]
Используя полиномы Баттерворта или формулу ( 17.7 а), записываем операторную передаточную функцию. [2]
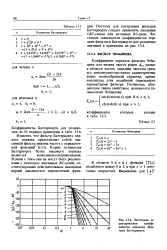 |
Частотные характеристики коэффициентов передачи фильтров Баттерворта. [3] |
Корни полиномов Баттерворта более высокого порядка являются комплексно-сопряженными. [4]
 |
Расположение полюсов при гладкой аппроксимации. [5] |
РВп называют полиномом Баттерворта n - й степени. Этот полином не требуется вычислять всякий раз, когда применяется гладкая аппроксимация. Такие полиномы могут быть раз и навсегда вычислены и представлены в табличной форме. В табл. 9 - 1 и 9 - 2 приводятся коэффициенты и сомножители полиномов Баттерворта для п10, когда угловая частота, соответствующая половинной мощности, нормализована до единицы. [6]
Применим для аппроксимации характеристики ФНЧ-прото-типа полиномы Баттерворта. [7]
При решении задачи аппроксимации полезно знать полиномы Баттерворта и Чебышева, которые приводятся ниже. [8]
На практике широко применяют аппроксимацию АЧХ полиномами Баттерворта, Чебышева и Бесселя. [9]
Решим задачу аппроксимации характеристики ФНЧ с помощью полиномов Баттерворта ( см. зад. [10]
Чтобы оценить bo, надо обратиться к табл. 1, где даны коэффициенты полинома Баттерворта шестой степени. [11]
 |
Соотношение между корнями фильтров Чебышева и Баттерворта. [12] |
При помощи этого соотношения можно вычислить корни полинома Чебышева, если известны соответствующие корни полинома Баттерворта. [13]
Найти операторные передаточные функции ПФ, требования к которым приведены в табл. 17.2, если аппроксимация выполняется с помощью полиномов Баттерворта. [14]
Изобразить примерные графики частотной зависимости ослабления, удовлетворяющие требованиям к ФНЧ ( рис. 17.4) при аппроксимации: а) полиномами Баттерворта; б) полиномами Чебышева пятого порядка, в) дробями Золотарева третьего порядка. [15]
Страницы: 1 2