Полином - порядок
Cтраница 2
 |
Элементы формулы Гаусса. [16] |
В качестве примера на рис. 75 приведено сопоставление интегрирований по Ньютон-Дотесу и Гауссу, обеспечивающего точ: ное вычисление интеграла для полиномов седьмого порядка. [17]
Таким образом, независимо от того, сходится ряд Фурье функции f ( x) по ортогональной системе на отрезке [ а, Ь ] к этой функции или нет, его п-я частная сумма дает наилучшее среднее квадратическое приближение функции f ( л) на этом отрезке по сравнению со всеми другими полиномами порядка п относительно данной ортогональной системы. [18]
N) мало пригодны для статистического анализа систем управления с большим числом ( т 50) случайных величин - возмущений. Fm) не может быть представлена полиномом невысокого порядка. [19]
В кодовых словах, выраженных в полиномиальной форме, циклическая природа кода проявляется следующим образом. Если U ( X) является кодовым словом, представленным полиномом порядка ( - 1), то U ( ( X) - остаток от деления X U ( X) на Х 1 - также является кодовым словом. [20]
Это имеет место для одноконтурных систем с управлением по отклонению и в некоторых других случаях. В остальных случаях N ( s) представляет собой обычно полином порядка не выше второго. [21]
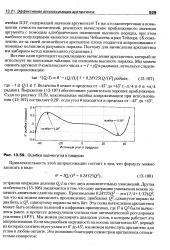 |
Ошибка оценки угла в градусах. [22] |
Те же, кто заинтересован в повышении точности вычислений, реализуют вычисление приближенного значения аргумента с помощью алгебраических полиномов высокого порядка, при этом наиболее популярными являются полиномы Чебышева и ряд Тейлора. К сожалению, из-за своей нелинейности арктангенс плохо поддается аппроксимации с помощью полиномов разумного порядка. Поэтому для вычисления арктангенса мы выбираем метод наименьшего ухудшения. [23]
При беспорядочном изменении табличных данных для каждого участка частотного диапазона следует подбирать свой аппроксимирующий многочлен. Для медленно изменяющихся функций при небольшой полосе частот и малой области изменения функций обычно достаточно ограничиться полиномами невысокого порядка. При широкой полосе частот и малой области изменения функций используют полиномы малого порядка в функциональной зависимости от логарифма частот. В случае весьма широких частотных полос и большого диапазона изменений функций следует перейти также к логарифмическому масштабу и использовать полиномную зависимость достаточно малого порядка. Аппроксимацию частотных характеристик целесообразно выполнять с помощью ортогональных функций. ЭВМ выполняются с ограниченным числом значащих функций, при которых пропадают значащие разряды. Отсюда следует, что при аппроксимации полиномами для вычислений необходимо использовать большее число знаков. [24]
С математической точки зрения большой теоретический интерес представляет создание алгоритмов, для которых можно было бы доказать гарантированную сходимость, хотя бы в обманчивых рамках действительной арифметики. С точки зрения практической имеется потребность в алгоритмах, которые бы почти всегда работали и вычисляли каждый нуль за малые доли секунды, если полином умеренного порядка, а машина достаточно мощная. [25]
Если входные переменные не коррелированы, процедура определения оптимальной в указанном смысле структуры регрессионной модели может сводиться, например, к тому, что рассматриваются полиномы порядка п - 1, а затем проверяется гипотеза о значимости различия остаточных дисперсий или значимости коэффициентов при переменной порядка га. [26]
Неравенства ( 22), ( 23) и ( 23) характеризуют в классе экспоненциальных полиномов, удовлетворяющих одним и тем же начальным условиям, полиномы наинизшего порядка. Ниже мы покажем, что это экстремальное свойство экспоненциальных полиномов сохраняется и в классе всех абсолютно монотонных функций. Представляет интерес убедиться в этом непосредственным сравнением дифференциальных уравнений ( 16) и ( 16), которым удовлетворяют экспоненциальные полиномы с соответствующими неравенствами. [27]
 |
Графики функции и ее интер - чтобы они удовлетворяли ус-поляционного приближения ЛОВИЯМ. [28] |
Полиномы такого вида называют интерполяционными полиномами Лагранжа, а функции Li ( x) - коэффициентами Лаг-ранжа. Поскольку при выводе формулы (2.20) было использовано только условие единственности приближающей функции и предположение, что qi ( x) в (2.15) являются полиномами i - ro порядка без конкретизации их вида, получим следующий вывод: независимо от способа определения интерполяционных полиномов из класса полиномов порядка не выше п они будут тождественно равны интерполяционному полиному Лагранжа. [29]
Для больших т Sm приближается к гауссиану в смысле центральной предельной теоремы. Sm является аналогом гауссиана для таких систем. Базовые функции Sm ( Xj - x) и, следовательно, F ( x) являются полиномами порядка т, как показано в подписи к рис. 8.2. Имеются т непрерывных производных. [30]
Страницы: 1 2 3