Полином - более высокая степень
Cтраница 2
Если в результате проверки установлено, что полученное уравнение не соответствует исследуемому явлению, то это значит, что либо неправильно выбран шаг варьирования, либо исследуемое явление следует описывать полиномом более высокой степени. [16]
В табл. 1 приведены условия устойчивости для полиномов до четвертой степени включительно. В случае полиномов более высокой степени проверка условий ( 27) требует вычисления определителей и проводится на ЭВМ по стандартной подпрограмме. [17]
Аппроксимация профиля температуры квадратичной зависимостью ( 17 - 49) приводит в случае стационарного режима к ошибке до i.4 % по сравнению с точным решением. Однако использование полинома более высокой степени не дает заметного улучшения результатов. [18]
Фурье приходится прибегать к аппроксимации полиномом более высокой степени или другими аналитическими функциями. Применение же представления характеристики ломаной линией здесь оказывается нерациональным из-за очень больших вычислительных трудностей. [19]
Математическая модель I порядка неадекватно описывает функционирование системы, так как два эффекта взаимодействия i 4 и х2 4 оказались значимыми. Следовательно, данная система должна быть описана полиномом более высокой степени. [20]
Формула Симпсона использует квадратичное приближение, когда площадь криволинейной трапеции заменяется суммой площадей параболических трапеций. Очевидно, имея в распоряжении набор точек, можно построить полином более высокой степени. Но при этом возрастает число требуемых узловых точек, и формулы становятся громоздкими. Вообще же выбор формулы для интегрирования определяется классом функций. Может оказаться, что формула более высокого порядка приведет к большим ошибкам. Например, при интегрировании линейных функций максимальная точность будет достигнута при использовании формулы трапеций. Представленные выше формулы являются частным случаем формул Ньютона-Котеса. [21]
Согласно Нильсону ( 1965), линейные разделяющие функции для случая двоичных независимых переменных ( и многомерных, распределенных по закону Бернулли) получены Дж. Если не требовать независимости переменных, то даже для случая бинарных переменных понадобятся полиномы более высоких степеней. [22]
Здесь следует отметить то обстоятельство, что матрица ( В В) является диагональной и, следовательно, может быть легко и точно обращена без ошибок, вызванных округлением. Эта отличительная черта оказывается особенно важной в тех случаях, когда проводится аппроксимация полиномом более высокой степени. [23]
Способ Польгаузена основан на аппроксимации распределения скоростей в пограничном слое полиномом четвертой степени. В связи с этим возникла мысль улучшить способ Польгаузена путем аппроксимации распределения скоростей полиномом более высокой степени. Конечно, при этом появляются дополнительные коэффициенты, вследствие чего выбранное распределение скоростей должно удовлетворять большему количеству граничных условий на стенке и на внешней границе пограничного слоя. Результаты, даваемые этим способом для параметров пограничного слоя и для положения точки отрыва, мало чем отличаются от результатов, получаемых посредством использования полинома четвертой степени. Другие случаи такого одно-параметрического представления распределения скоростей рассмотрены и сравнены с точными решениями в работе В. Для аппроксимации распределения скоростей возможно применение не только полиномов, но и других выражений. Такие возможности были испробованы рядом исследователей. [24]
Изложенные в предыдущем параграфе методы, основанные на локально-линейном приближении поверхности отклика, хотя и обеспечивают быстрое достижение почти стационарной области, но не дают возможности детального ее изучения и определения самого экстремума. Так как линейное описание поверхности отклика в почти стационарной области становится неадекватным, ее приходится приближать полиномами более высокой степени d ( обычно второй, реже третьей и четвертой степени), учитывающими кривизну поверхности отклика. X sk ( при равном количестве уровней - ПФЭ типа s f) оказывается практически невозможным из-за большого количества опытов. Поэтому актуальна задача оптимального расположения экспериментальных точек в изучаемой области. В зависимости от степени приближающего полинома разработаны эффективные планы второго, третьего и четвертого порядков. [25]
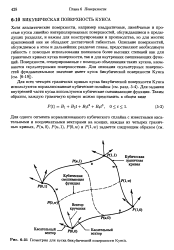 |
Геометрия для куска бикубической поверхности Кунса. [26] |
Хотя аналитические поверхности, например квадратичные, линейчатые и простые куски линейно интерполированных поверхностей, обсуждавшиеся в предыдущих разделах, и важны для конструирования и производства, но для многих приложений они не обладают достаточной гибкостью. Описание поверхностей, обсуждаемое в этом и дальнейших разделах главы, предоставляют необходимую гибкость с помощью использования полиномов более высоких степеней как для граничных кривых куска поверхности, так и для внутренних смешивающих функций. Поверхности, сгенерированные с помощью объединения таких кусков, называются скульптурными поверхностями. [27]
Основная особенность этого метода состоит в том, что в виде полинома представляются не коэффициенты активности компонентов или давления пара, а функция GE ( x), которая обычно имеет более простой вид. В работе [91 ] показано, что для описания зависимости g ( А:) достаточно использовать полиномы третьей или четвертой степени. Привлечение полиномов более высоких степеней приводит к увеличению вычислительных погрешностей. [28]
Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях - полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку. [29]
Это значит, что мы попали в область, близкую к оптимуму. Здесь линейная модель уже не нужна. Либо попаданием в почти стационарную область задача решена, либо надо переходить к полиномам более высоких степеней, например, второй степени. [30]
Страницы: 1 2 3