Алгебраический полином

Cтраница 2

Совершенно так же доказывается счет-ность множества всех алгебраических полиномов с рациональными коэффициентами, зависящих от любого числа переменных. [16]

Наиболее употребительными в теории приближения функций полиномами являются тригонометрические и алгебраические полиномы. [17]

Рассмотрим наиболее простой полуобратный метод решения с помощью целых алгебраических полиномов различных степеней. Сущность метода состоит в том, что функцию ц ( х у) задают в виде полинома, коэффициенты которого подбираются так, чтобы удовлетворялось ( энгармоническое уравнение (17.22) и граничные условия. [18]

Представление об аналитичности функ Г к отклика позволяет выбирать алгебраические полиномы в качестве базовых моделей, как наиболее простых. Это соглашение базируется на накопленном разными исследователями опыте работы с такими моделями и обычно удовлетворяют экспериментатора. Кроме того, полином линеен относительно неизвестных коэффициентов, что упрощает обработку наблюдений. [19]

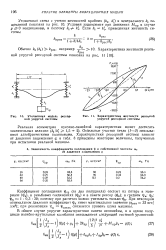Характеристика жесткости реальной упругой рессорной системы. [20]

Отдельные участки петли ( 1 - 5) описываются алгебраическими полиномами. Характеристики рессорной системы зависят от давления защемления q; в табл. 8 приведены некоторые величины, полученные при испытании реальной машины. [21]

Фиксируем порядок TV всех строящихся полиномов Фурье и степень s алгебраических полиномов для их коэффициентов, а также допустимую погрешность Д коэффициентов. [22]

Исторически и прагматически наиболее важным классом интерполирующих функций является множество алгебраических полиномов. [23]

Вещественное число называется алгебраическим, если оно является корнем некоторого алгебраического полинома с целыми коэффициентами. [24]

В других случаях их аппроксимируют, например, в виде алгебраических полиномов с целыми степенями. [25]

Рассмотрим примеры построения решений обратной плоской задачи теории упругости с помощью алгебраических полиномов. [26]

Программа S1POLI реализует алгоритм РПС восстановления решения интегрального уравнения в виде алгебраического полинома оптимальной степени, которая определяется в процессе вычислений, е одновременной селекцией наблюдений. Алгоритм РПС описан в § 2 гл. [27]

Если N О, то проводятся дополнительные преобразования фундаментальных сплайнов для построения алгебраического полинома степени меньше кубической. [28]

Программа POLILL реализует алгоритм РП построения приближенного решения интегрального уравнения в виде алгебраического полинома оптимальной степени, которая определяется в процессе выполнения алгоритма. Алгоритм РП описан в § 2 гл. [29]

Та степень, при которой оценка принимает наименьшее значение, является оптимальной степенью алгебраического полинома, приближающего решение интегрального уравнения. Сам этот полином определяется набором коэффициентов а, являющимся решением нормальной системы, которая соответствует оптимальной степени полинома. [30]

Страницы: 1 2 3 4