Алгебраический полином

Cтраница 3

В нем счетным всюду плотным множеством является, например, множество & всех алгебраических полиномов с рациональными коэффициентами. [31]

При интегрировании конечно-разностными методами наибольшее распространение получили формулы, в которых решение аппроксимируется алгебраическими полиномами. В частности, формулы Ньютона - для интерполирования назад ( формула 11 - 29) используются в методе Адамса, а формулы Ньютона для интерполирования вперед ( формула 11 - 28) - в методе Милна. [32]

При интегрировании конечно-разностными методами наибольшее распространение получили формулы, в которых решение аппроксимируется алгебраическими полиномами. [33]

Если исследуемый процесс в ( /) является монотонной функцией, то следует выбрать алгебраический полином или линейную комбинацию ортогональных полиномов, которые также представляют собой монотонные функции. Если исследуемый процесс имеет колебательный характер, то целесообразна аппроксимация тригонометрическими полиномами. Если же процесс имеет колебательную и монотонную составляющие одновременно, то для аппроксимации рекомендуются полиномы Лежандра. [34]

Осредпепные сплайны, получаемые в результате выполнения алгоритма СР, имеют существенные преимущества перед алгебраическими полиномами, получаемыми с помощью алгоритма ПР. [35]

Хотя книга, как сказано выше, посвящена в основном вопросам равномерного приближения функций алгебраическими полиномами, в первых параграфах изложение ведется в более общем плане. Это, с одной стороны, позволяет лучше уяснить сущность рассматриваемых свойств, а с другой - приводимые здесь результаты представляют для вычислителя и самостоятельный интерес. Довольно большое внимание в курсе уделяется вопросам приближения периодических функций тригонометрическими полиномами. Известные результаты здесь более полны, чем для случая приближения алгебраическими многочленами, и служат базой для получения соответствующих результатов в алгебраическом случае. [36]

Значения коэффициентов аппроксимирующих полиномов для перечисленных зависимостей приведены в безразмерном виде в табл. 1.1. Использование алгебраических полиномов при проведении расчетов удобно потому, что наряду с вычислением по схеме Горнера значения функции вычисляется значение и ее производной. [37]

Символы операций с постоянными коэффициентами вида ( 1) обладают свойствами, сближающими нх с алгебраическими полиномами. [38]

При решении плоской задачи с помощью функции напряжений применяются различные методы: полуобратный метод с использованием алгебраических полиномов или тригонометрических рядов, метод функций комплексных переменных, метод конечных разностей ( § 21.1) и другие методы. [39]

РП показала, что использование сплайнов для приближенного решения интегральных уравнений более эффективно, чем использование алгебраических полиномов. С другой стороны, программная реализация алгоритма РГ1 более экономна, чем алгоритма PC по необходимому времени вычислений. [40]

Если число сопряжений сплайна N 0, то производятся дополнительные преобразования образов фундаментальных сплайнов для построения алгебраического полинома степени меньше кубической. [41]

Зависимости физических свойств фаз от давления, использованные при решении системы (105.12), были приняты в виде алгебраических полиномов, построенных на основании физических данных изучения этих свойств в лабораторных условиях по пробам газа, нефти, конденсата и воды из рассматриваемого месторождения. Исходные данные по свойствам флюидов были следующие: ргст. [42]

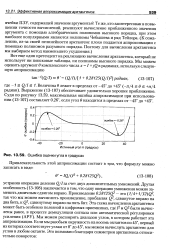Ошибка оценки угла в градусах. [43]

Те же, кто заинтересован в повышении точности вычислений, реализуют вычисление приближенного значения аргумента с помощью алгебраических полиномов высокого порядка, при этом наиболее популярными являются полиномы Чебышева и ряд Тейлора. К сожалению, из-за своей нелинейности арктангенс плохо поддается аппроксимации с помощью полиномов разумного порядка. Поэтому для вычисления арктангенса мы выбираем метод наименьшего ухудшения. [44]

Значения коэффициентов и соответствующих производных в точке ( i, j) в безразмерном виде вычисляются по заранее подобранным алгебраическим полиномам. [45]

Страницы: 1 2 3 4