Понижение - размерность
Cтраница 3
В общем случае, когда не применимы описанные выше схемы пласта, допускающие понижение размерности задачи, с этой целью используются динамические модифицированные фазовые проницаемости. [31]
Этот недостаток особенно ощутим в случае высокоразмерных задач, когда универсальные эвристики становятся малоэффективными ( например, понижение размерности задачи с 21000 до 2100 не обеспечивает возможность практического решения задачи на ЦВМ), а поиск специализированных эвристик является искусством, не всегда приводящим к решению. [32]
Методам ГИУ посвящен сборник [1]; там же в дополнении рассмотрены и некоторые возможности применения вариационных методов для понижения размерности краевых задач и их последующего численного решения, а также даны ссылки на работы советских ученых в рассматриваемой области. Сборник был призван в первую очередь стимулировать интерес инженеров, механиков и физиков к этим методам. [33]
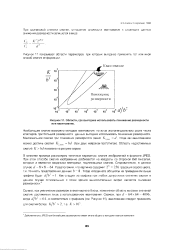 |
Области, где выгоднее использовать понижение размерности или квантование. [34] |
Наибольшее сжатие возможно методом квантования; но из-за экспоненциального роста числа кластеров; при большой размерности данных выгоднее использовать понижение размерности. [35]
 |
Зависимость безразмерной эффективной проницаемости области с застойными зонами v от параметра р при различных коэффициентах вариации проницаемости. [36] |
Однако в плоском случае функции о и v убывают несколько быстрее, что объясняется повышением роли застойных зон, связанных с понижением размерности пространства. [37]
Основной особенностью является появление зависимости диффузионной константы скорости ( и, в частности, константы квадратичного обрыва) от времени, причем с понижением размерности реакционной зоны эта зависимость усиливается. Другой интересной особенностью является зависимость среднего времени жизни активных центров на поверхности от ее структурных свойств. Этот результат является следствием весьма общих обстоятельств, связанных о особенностями диффузии на фракталах. [38]
Поэтому в общем случае при учете различных взаимных междуфазных индуктивностей, различных фазных активных сопротивлений и сопротивлений самоиндукции применение симметричных составляющих не приводит к понижению размерности систем уравнений, решаемых при расчете установившегося режима. Таким образом, параметры элементов сети иногда проще определяются в системе фазных координат. Достоинство метода симметричных составляющих в том, что с его помощью проще определяются показатели несимметрии - составляющие обратной и нулевой последовательностей напряжений и токов. Это важно, поскольку для проверки требований по качеству напряжения в соответствии с ГОСТ необходимо вычислить эти показатели несимметрии. [39]
Приведенные некоторые возможные траектории ( / - линейная; II - криволинейная; / / / - ломаная) нагружения в точке деформируемого тела и случаи понижения размерности изображающих пространств связаны со специальными геометрическими свойствами тел и специальных видов нагрузок независимо от физических свойств материала рассматриваемых тел и законов изменения нагрузок во времени. Однако, задавая различные законы изменения нагрузок, получаем различные траектории нагружения. Тогда и траектории нагружения в каждой точке одинаковы. В общем случае твердые тела под воздействием объемных и поверхностных сил находятся в условиях неоднородного напряженного состояния. Поэтому для тела в целом получим пучок траекторий с соответствующими физическими векторами. [40]
Видно, что значения К, полученные для двумерных решеток, существенно больше, чем для трехмерных, что вполне согласуется с приведенными выше представлениями об усилении роли самопересечений с понижением размерности блуждания. Из приведенных данных также видно, что ограничение числа возможных направлений шага на решетке приводит к уменьшению А. Это ограничение может моделировать возрастание жесткости цепи, которое связано с возрастанием доли вытянутых конформаций. Интересно заметить, что толщину цепи в рамках модели случайного блуждания можно учитывать посредством запрета контактов траектории на соседних узлах решетки, что также увеличивает А. [41]
Модуль А когомологически тривиален тогда и только тогда, когда для нек-рого гЯ ( Я, А) 0 и Я 1 ( Я, А) 0 для любой подгруппы Я.С. Любой модуль А можно представить как подмодуль или фактормодуль когомологически тривиального модуля, что позволяет применять сдвиг размерностей как для повышения, так и для понижения размерности. Для конечно порожденного G-модуля А группы Я ( С, А) конечны. [42]
Как будет отмечено в следующем разделе, в методе ГИУ оперируют только граничными значениями, что на единицу понижает размерность задачи. Это понижение размерности значительно сокращает объем памяти и время работы центрального процессора, которые необходимы для решения задачи на ЭВМ. В методе ГИУ связь компонент вектора напряжений на границе с граничными перемещениями устанавливается при помощи системы интегральных уравнений, которую требуется численно преобразовать к алгебраической системе и решить численно. [43]
Задача распределения п сортов хлора по потребителям с учетом указанных ограничений и критерия оптимизации ( прибыли) решается методом динамического программирования. Для понижения размерности используется метод неопределенных множителей Лагранжа. [44]
Поскольку р ( х) имеет корень в F, DI F - не тело. Продолжая это понижение размерностей, мы получим в конце концов такое поле L, что AL - расщепимая алгебра. [45]
Страницы: 1 2 3 4