Понятие - вероятность
Cтраница 3
Все внимание привлекло понятие вероятности случайного события. [31]
Предварительно необходимо рассмотреть понятие вероятности состояния термодинамической системы. [32]
Данное выше определение понятия вероятности может быть уточнено с помощью закона больших чисел; в частности, можно записать в математической форме утверждение, что относительная частота появления события, вообще говоря, тем ближе к константе, чем больше число испытаний. [33]
Исчерпывающей математической формулировки понятия вероятности не существует. [34]
Все возможные определения понятия вероятности весьма неполно отражают реальную практику. [35]
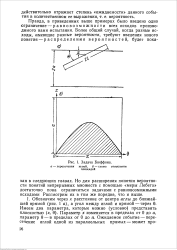 |
Задача Бюффона. [36] |
Но для расширения понятия вероятности понятий непрерывных множеств с помощью меры Лебега достаточно пока ограничиться задачами с равновозможными исходами Рассмотрим их в том же порядке, что и выше. [37]
Подойдем теперь к понятию вероятности более формально. [38]
В сильно неравновесных условиях понятие вероятности, лежащее в основе больцмановского принципа порядка, становится неприменимым: наблюдаемые структуры не соответствуют максимуму комплексов. Не соответствует максимум комплексов и минимуму свободной энергии F E-TS. Тенденция к выравниванию и забыванию начальных условий перестает быть общей тенденцией. В этом смысле старая проблема происхождения жизни предстает в ином свете. Заведомо ясно, что жизнь несовместима с принципом порядка Больцмана, но не противоречит тому типу поведения, который устанавливается в сильно неравновесных условиях. [39]
Классическое определение вероятности сводит понятие вероятности к понятию равновероятности ( равновозможности) событий, которое считается основным и не подлежит формальному определению. [40]
В двух крайних случаях понятие вероятности формально применяют по отношению к событиям, не являющимся случайными. Если некоторое событие никогда не происходит, его называют невозможным событием и полагают его вероятность равной нулю. Другой крайний случай связан с событием, которое при определенных условиях происходит наверняка. Такое событие называют достоверным и полагают его вероятность равной единице. Конечно, ни невозможное, ни достоверное события нельзя считать случайными. Невозможное событие попросту не существует; мы можем говорить о нем лишь чисто умозрительно. Примеры невозможных событий: железный молоток при нагревании подскочил вверх; упавшее с яблони яблоко превратилось в грушу; при совершенно безоблачном небе пошел сильный дождь. Что же касается достоверных событий, то они по самой сути своей не являются случайными - они происходят наверняка. [41]
С каждым событием связывают понятие вероятности - числовой характеристики объективной возможности появления события. Существуют события, вероятность которых можно определить из условий самого опыта, не производя его. Говорят, что в этом случае опыт сводится к схеме случаев. Случай называется благоприятствующим некоторому событию А, если появление этого случая влечет за собой появление данного события А. [42]
В данной главе рассматривается понятие вероятности и ее применение в различных хозяйственных ситуациях. Вероятность используется для отражения возможности наступления альтернативных событий в условиях неопределенности. Руководитель может получить преимущество, если он знаком с методами определения вероятности и использует их при принятии решений. [43]
В 1 -и главе рассмотрено понятие вероятности, случайного события, случайной величины, дано определение закона распределения случайной величины, а также изучены основные параметры законов распределения, такие как показатели центра распределения, показатели меры рассеяния, показатели формы распределения. [44]
В сильно неравновесных условиях понятие вероятности, лежащее в основе больцмановского принципа порядка, становится неприменимым: наблюдаемые структуры не соответствуют максимуму комплексов. Не соответствует максимум комплексов и минимуму свободной энергии РЕ-Г5. Тенденция к выравниванию и забыванию начальных условий перестает быть общей тенденцией. В этом смысле старая проблема происхождения жизни предстает в ином свете. Заведомо ясно, что жизнь несовместима с принципом порядка Больцмана, но не противоречит тому типу поведения, который устанавливается в сильно неравновесных условиях. [45]
Страницы: 1 2 3 4