Понятие - градиент
Cтраница 1
Понятие градиента входит в формулировку основного закона теплопроводности и поэтому заслуживает более подробного рассмотрения. [1]
 |
К рассмотрению внутреннего ствующая перемещению слоев трения жидкостей. жидкости, а значит, и пла. [2] |
Понятие градиента было пояснено на стр. [3]
 |
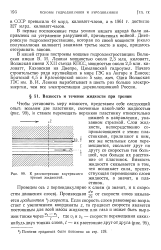
Линии равной температуры.| К определению понятия градиента. [4] |
Понятие градиента входит в формулировку основного закона теплопроводности и поэтому заслуживает более подробного рассмотрения. [5]
С понятием градиента тесно связано понятие потенциального векторного поля. [6]
Если применить понятие градиента к самонастраивающимся системам управления, то функцию Q следует рассматривать как некоторый критерий, являющийся функцией настраиваемых параметров щ системы. [7]
 |
Блок-схема х - х - - a grad Q ( x, алгоритма градиентного. [8] |
Идея использования понятия градиента для целей убыстрения поиска заключается в следующем. [9]
 |
К выводу уравнения коэффициента диффузии. [10] |
IX было введено понятие градиента концентрации. [11]
Введенные в этой главе понятия градиента, ротора, дивергенции, а также полученные формулы Грина, Стокса, Остроградского - Гаусса находят широкое применение в физических и технических приложениях, связанных с рассмотрением реальных физических полей. [12]
Именно этот факт придает понятию градиента большое значение. Поставим, например, вопрос: в каком направлении функция / быстрее всего возрастает или быстрее всего убывает. Для ответа на этот вопрос надо найти то направление, на которое проекция градиента имеет наибольшее положительное или наибольшее по абсолютной величине отрицательное значение. Первое будет, очевидно, когда вектор с имеет направление градиента, второе - когда направление с прямо противоположно направлению градиента. [13]
В курсе математики пользуются понятием градиента скалярной функции. Градиентом скалярной функции называют скорость изменения скалярной функции, взятую в направлении ее наибольшего возрастания. [14]
В курсе математики пользуются понятием градиента скалярной функции. Градиентом скалярной функции называют скорость изменения скалярной фуякции, взятую в направлении ее наибольшего возрастания. [15]
Страницы: 1 2 3