Понятия - устойчивость
Cтраница 2
Устойчивость, выраженную оценкой ( 10), называют устойчивостью по начальным данным и по правой части. Используются также понятия устойчивости по начальным данным и устойчивости по правой части. [16]
В статье [20] рассмотрена устойчивость в большом и в целом. Известно, что понятия устойчивости, чувствительности и инвариантности характеризуют работу системы с разных сторон. [17]
В параграфе 3.1 формируются основные результаты метода сравнения в терминах функций типа функций Ляпунова и теории дифференциальных, неравенств, которые необходимы для дальнейшего изложения. В параграфе 3.2 определены понятия устойчивости в терминах двух различных мер и показано, как эти понятия позволяют унифицировать разнообразие понятий устойчивости, встречающихся в литературе. В параграфе 3.3 предложены достаточные условия для различных типов устойчивости в терминах двух мер. В этом параграфе также вводятся семейства функций Ляпунова для изучения свойств равномерной устойчивости, когда обычные предположения могут быть ослаблены. В этом общем направлении рассматриваются обобщения теоремы В. В параграфе 3.4 доказана теорема обращения для равномерной асимптотической устойчивости в термина - k двух мер, которое включает хорошо известную обратную теорему Массеры. Вследстаие связи между двумя мерами, подтверждается то, что построение гладкой функции Ляпунова возможно при умеренных предположениях. Интересно, что рассматриваемая теорема обращения приводит, в частности, к обратной теореме о частичной равномерной асимптотической устойчивости и, таким образом, обеспечивает достаточно гибкий результат, чтобы оправдать его применение в нескольких направлениях. В параграфе 3.5 указываются критерии ограниченности и устойчивости по Лагранжу в терминах двух мер. [18]
Однако в нелинейных системах большее значение имеет устойчивость в некоторой области, характеризующаяся возвратом системы в заданную область при уменьшении внешнего воздействия до нуля. При оценке устойчивости обоих видов применяют понятия устойчивости в малом, в большом ( см. гл. I части I) и в целом, введенные в связи с рассмотрением процессов в нелинейных системах. Все виды устойчивости будут рассмотрены далее при анализе различными методами конкретных систем управления. [19]
Проблемы анализа банковской деятельности в той или иной степени отражены в трудах таких отечественных специалистов и ученых, как Л.Г. Батракова, И.Д. Мамонова, Ю.С. Масленченков, Г.С. Панова, Г.Г. Фетисов, А.Д. Шеремет и др. Предлагаемые всеми авторами методики, как правило, включают следующие основные направления анализа: ликвидность, достаточность капитала, качество активов и пассивов, прибыльность банка. При этом следует отметить, что понятия устойчивости и надежности банка не являются синонимами, каждое из них имеет свою специфику и область применения. Под устойчивостью коммерческого банка ( КБ) понимается его способность выполнять на заданном обществом уровне присущие ему функции и роль в экономике вне зависимости от воздействия внешних и внутренних факторов. Надежным банком является банк, деятельность которого, несомненно, приводит к реализации интересов конкретного субъекта. Это понятие более целесообразно использовать с позиции предприятия как клиента, вкладчика, инвестора, партнера банка. Надежный банк может не быть устойчивым, при этом устойчивый банк, как правило, надежный. [20]
Описанные особенности устойчивости нелинейных систем требуют при рассмотрении устойчивости таких систем оговаривать начальные условия и внешние воздействия, как это делалось ранее при рассмотрении качества линейных систем. В связи с этим при изучении нелинейных систем употребляются понятия устойчивости в малом, в большом и в целом. [21]
Таким образом, функции г ( t, х) ( как и в системе (1.9)) имеют смысл постоянно действующих возмущений. О, может, в общем случае, отличаться от понятия устойчивости по Ляпунову системы обыкновенных дифференциальных уравнений, или других понятий устойчивости систем обыкновенных дифференциальных уравнений. [22]
Но зачем было рассматривать П - регуляторы со всеми их недостатками, если известно, как эти недостатки устранить, неужели все дело только в непонятном пристрастии авторов к древностям. Ответ на этот вопрос приводит нас к рассмотрению нового понятия - понятия устойчивости. Не встретит ли здесь читатель еще кого-нибудь из своих старых знакомых, хотя, может быть, и не упомянутых еще на страницах этой книги. Ведь груз, укрепленный на рычаге, способном свободно качаться на шарнире, - это обыкновенный маятник. Правда, маятник несколько своеобразный, поскольку в данном случае кроме силы, веса на него действует еще и центробежная сила, и поэтому в состоянии равновесия рычаг несколько отклонен от вертикали. Однако он сохраняет все свойства маятника. В частности, испытав толчок, он начинает совершать колебания относительно положения равновесия. [23]
В параграфе обсуждается ряд вопросов, связанных с анализом устойчивости нулевого состояния равновесия динамических систем. Различаются понятия устойчивости по Ляпунову, асимптотической устойчивости и абсолютной устойчивости по отношению к некоторому классу уравнений. Теория устойчивости составляет хорошо развитую главу механики, теории управления, математики с мощными методами исследования и разнообразными важными результатами, относящимися к системам, описываемым эволюционными уравнениями различных классов. [24]
На первый взгляд устойчивость равновесия и устойчивость движения принципиально различны. С физической точки зрения это так и есть. Однако математически оба эти понятия устойчивости находят идентичную трактовку. [25]
Ядро дейтерия состоит из протона и нейтрона. Как частица, дейтон совершенно устойчив. Этот пример показывает, что понятия устойчивости и элементарности - не тождественны. [26]
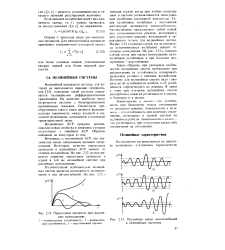 |
Переходные процессы при различных возмущениях.| Различные виды автоколебаний в нелинейных системах. [27] |
Таким образом, при указанных особенностях нелинейных систем необходимо при рассмотрении их устойчивости оговаривать начальные условия и внешние воздействия. В связи с этим при изучении нелинейных систем употребляют понятия устойчивости в малом, в большом и в целом. [28]
Ядро дейтерия состоит из протона и нейтрона. Как частица, дейтон совершенно устойчив. В то же время составная часть дей-тона, нейтрон, - радиоактивен, т.е. неустойчив. Этот пример показывает, что понятия устойчивости и элементарности - не тождественны. [29]
Выше при определении различных понятий устойчивости мы руководствовались тем, как изменяется со временем расстояние p [ y ( t) y ( t) ] y ( t) - y ( t) между изображающими точками этих движений. Однако если невозмущенное движение является периодическим и совершается по замкнутой траектории ( например, движение небесных тел), то важно, как ведет себя изображающая точка возмущенного движения относительно траектории невозмущенного движения, а не относительно его изображающей точки. Поэтому при рассмотрении периодических процессов используются понятия устойчивости, отличные от рассмотренных выше, - орбитальная устойчивость и асимптотическая орбитальная устойчивость. [30]
Страницы: 1 2 3