Периодический потенциал

Cтраница 4

Соизмеримые и несоизмеримые волны зарядовой плотности. а - для случая наполовину заполненной зоны. б - эквивалентная конфигурация ВЗП для наполовину заполненной зоны. в - несоизмеримая ВЗП. г - ВЗП в модели желе. Модель желе основана на представлении об ансамбле электронов, движущихся в поле однородно распределенного положительного заряда.| Фононная дисперсионная зависимость ш w ( A. Сплошной линией показана нормальная дисперсионная кривая акустических фононов. Штриховые линии иллюстрируют эффект понижения частоты колебаний с волновым вектором А 2kj., обусловленный экранирующим воздействием электронов проводимости. В точке А 2А /. частота понижается с понижением температуры. [46]

Оно возникает из-за того, что ВЗП приводит к появлению дополнительного периодического потенциала, в котором движутся ядра положительных ионов. [47]

Физическое содержание этого понятия сводится к тому, что влияние периодического потенциала кристаллической решетки на движение электрона может быть разным при движении электрона в разных направления и что вектор ускорения, вообще говоря, Не, совпадает по направлению с вектором внешней силы. В полупроводниках почти всегда электроны в зоне проводимости располагаются вблизи дна зоны, а дырки - у потолка валентной зоны. В общем же случае, вдали от этих областей, понятие эффективной массы - сильно усложняется, но эти случаи для полупроводников представляют малый практический интерес. [48]

В первом порядке по HF эти поправки согласно теории возмущения периодическим потенциалом ( см., например, Ландау и Лифшиц. [49]

Мы рассматриваем зону с наинизшей энергией в нашей задаче с периодическим потенциалом. В пределе больших т в сумме 2 в (10.10) доминирует эта зона. [50]

Потенциальная энергия электрона в металле. [51]

Изображая металл в виде потенциального ящика с гладким дном, мы заменяем периодический потенциал его средним значением, что оказывается, однако, вполне допустимым приближением при рассмотрении явлений электронной эмиссии. [52]

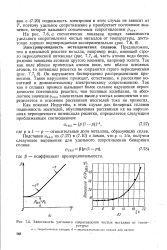Зависимость удельного сопротивления чистых металлов от температуры. [53]

Предположим, что в идеальной решетке металла, например меди, имеющей строго периодический потенциал ( рис. 7.7, а), часть атомов меди беспорядочно замещена атомами другого элемента, например золота. Он нарушается беспорядочно распределенными примесями. Такое нарушение приводит, естественно, к рассеянию носителей и дополнительному электрическому сопротивлению. Так как в сплавах примеси вызывают более сильное нарушение периодичности потенциала решетки, чем тепловые колебания, то абсолютное значение рспл значительно выше р чистых компонентов и определяется в основном рассеянием носителей тока на примесях. [54]

На рис. 30 [2] показано чередование разрешенных энергетических зон и щелей для периодического потенциала. [55]

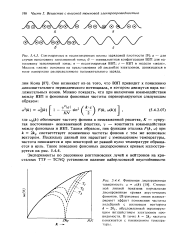
В соответствии с формулами (4.40) и (4.48) если электроны находятся в поле периодического потенциала, то на границе зоны Бриллюэна секулярное уравнение имеет два корня, и это соответствует тому, что электроны могут находиться в двух энергетических состояниях с расстоянием между ними 2С / К. Легко сообразить, что при малых k большие значения C ( g / 2) могут встречаться только для одной из волн. Это видно из уравнения (4.34), поскольку если знаменатель обращается в нуль, скажем, при fe 0, то вблизи любого из k g он будет достаточно большим. Общий вид закона дисперсии e ( k) изображен на рис. 4.4, который показывает, что в энергетическом спектре электронов возникают зоны разрешенных и запрещенных энергий. [56]

Страницы: 1 2 3 4