Пластический потенциал

Cтраница 1

Пластический потенциал Ф ( функция нагружения) может отличаться от функции, стоящей в левой части условия текучести. Однако обычно их отождествляют, ив этом случае закон течения называется ассоциированным. [1]

Пластический потенциал введем как функцию инвариантов тензора напряжений, определяющих пластическое а деформирование. [2]

Пластический потенциал S и функция текучести / - вообще различные и подбираются согласно экспериментальным данным. Можно, в частности, учесть упрочнение, если полагать, что поверхность текучести увеличивается, оставаясь подобной самой себе, по какому-нибудь закону, скажем пропорционально мощности пластической деформации. [3]

Закон течения пластического потенциала остается неизменным. [4]

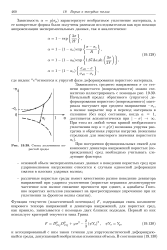Схема уплотнения пористой среды. [5]

Функция текучести ( пластический потенциал) F, содержащая связь компонент шарового тензора напряжений и девиатора напряжений, для пористых сред, как правило, записывается с помощью двух близких подходов. [6]

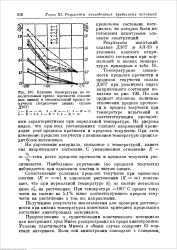Влияние температуры на относительный предел прочности ( сплошные линии и относительный предел текучести ( штриховые линии сплава Д16Т. [7]

Предположение о существовании пластического потенциала для изотропных сред Мизес распространил на среды анизотропные. Условие пластичности Мизеса в общем случае содержит 15 констант материала. [8]

Следовательно, в теории пластического потенциала направления характеристик поля напряжений и характеристик поля скоростей совпадают. [9]

Случай совпадения поверхностей текучести и пластического потенциала является простейшим и наиболее важным. Здесь следует остановиться на одном затруднении. При условии S / считается как бы само собой разумеющимся, что поверхность текучести имеет единственную нормаль в каждой точке. Это не всегда так; в частности, условие текучести Треска - Сен-Венана представляет поверхность шестигранной призмы ( § 9), и нормаль вдоль ребер неопределенна. Так как использование условия текучести Треска - Сен-Венана нередко приводит к значительным математическим упрощениям, то возникает важный вопрос о формулировке соответствующей зависимости между скоростями деформации и напряжениями. [10]

Мизес [599] распространил предположение о существовании пластического потенциала для изотропных сред на среды анизотропные, считая при этом материал несжимаемым и неупрочняющимся. [11]

К суть у-мерные векторы пластических множителей, пластических потенциалов ( предполагаемых линейными) и положительных постоянных соответственно для всех ( у ] режи - мов-течения в конструкции, с подразделением по элементам в том же порядке. [12]

Два соотношения (3.6) могут быть использованы в качестве пластического потенциала. [13]

Выше было показано, как можно применить теорию пластического потенциала к граням призмы Треска, где действительно существует единственным образом определенная нормаль. [14]

Обобщением результатов Мизеса явилось построение так называемой теории обобщенного пластического потенциала, принадлежащее Койтеру. Согласно Койтеру, угловые точки поверхности условия пластичности интерпретируются как предельные для соответствующих гладких поверхностей; поэтому в угловых точках направление вектора приращений пластических деформаций может принимать любое направление, ограниченное нормалями касательных плоскостей к точкам, лежащим как угодно близко к угловым. [15]

Страницы: 1 2 3