Замена - ядро
Cтраница 1
Замена ядра вырожденным может быть выполнена различными способами. [1]
Метод замены ядра на вырожденное. [2]
Это эквивалентно замене ядра уравнения (8.15) на вырожденное. [3]
Применение метода моментов равносильно замене ядра К ( х, s) вырожденным ядром Кп ( х, s), строящимся следующим образом. Предполагая орто-нормированность системы ф, ( х), разлагают ядро К ( х, s) как функцию х в ряд Фурье по этой ортонормированной системе функций и в качестве Кп ( х, s) принимают п-ю частичную сумму этого ряда. [4]
Можно ожидать, что при замене ядер, на которых ведется наблюдение ( например, при переходе от наблюдения за релаксацией ядер ионов 7Li к 19F), кроме размеров частиц, в состав которых входят парамагнитные ядра, большое влияние на релаксацию будут оказывать заряды парамагнитного иона и частицы. [5]
Сопряжеиное уравнение получается из данного заменой ядра: / сопряженным и параметра - комплексяб-еопряженным права часть, g ( x), совершенно произвольна. [6]
Стремление уменьшить количество воспроизводимых функций при замене ядра вырожденным усложняет применение приближений в виде рядов и интерполяционных формул. [7]
Рассмотрим решение интегральных уравнений Фредгольма второго рода методом замены ядра на вырожденное. [8]
Интегральное уравнение, полученное из ( 1) заменой ядра K ( x t) на K ( t x), называется союзным с ( 1) или транспонированным к нему. [9]
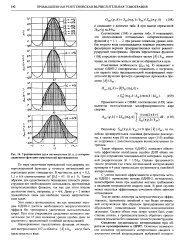 |
Традиционные ( а и оптимальные ( б, в, г интерполяционные функции ограниченной протяженности. [10] |
& м, то подобная предварительная линейная фильтрация реализуема, а замена ядра ( 8) на оптимальное ядро ( 110) вообще не сопряжена с дополнительными вычислительными затратами. [11]
При этом возникает вопрос: как влияет на решение уравнения такая замена ядра. [12]
Второй метод, также применимый в ряде случаев, это - замена ядра на вырожденное и сведение таким образом задачи опять к алгебраической системе. [13]
После этого эффективным оказывается метод простой итерации в сочетании с методом замены ядра на вырожденное. Особенности аналитической ( и геометрической) структуры ядер учитываются в методах [101], сводящих задачу решения интегральных уравнений к решению линейных алгебраических систем. [14]
На этой теореме основан метод приближенного решения интегральных уравнений Фредгольма с помощью замены ядра К ( t, s) близким к нему вырожденным ядром. [15]
Страницы: 1 2 3