Замена - ядро
Cтраница 2
Интегральные уравнения, полученные из ( 5) - ( 8) заменой ядра К ( х - t) на K ( t - ж), называются союзными с ними или транспонированными к ним. [16]
Интегральные уравнения, полученные из ( 2) - ( 5) заменой ядра К ( х - t) на K ( t - ж), называются союзными с ними или транспонированными к ним. [17]
Интегральные уравнения, полученные из ( 5) - ( 8) заменой ядра K ( x - t) на K ( t - x), называются союзными с ними или транспонированными к ним. [18]
Интегральные уравнения, полученные из ( 2) - ( 5) заменой ядра K ( x - t) на K ( t - x), называются союзными с ними или транспонированными к ним. [19]
Все они применимы к решению уравнения (6.1) и по существу являются различными модификациями метода замены ядра на вырожденное с одновременной подходящей аппроксимацией правой части уравнения. [20]
Для приближенного решения уравнений ( 44), ( 46) можно использовать рассмотренный выше метод замены ядра интегрального уравнения на близкое вырожденное. Следует заметить, что поскольку в уравнениях ( 44), ( 46) ядро интегрального оператора зависит от разности аргументов, то можно использовать более простой способ построения вырожденного ядра на основе полных ортонормированных систем функции, чем в случае ядра общего вида. Рассмотрим какой-либо элементТ в матрице-функции, являющейся ядром интегрального оператора В. [21]
ПОЛОС МЕТОД - метод приближенного решения одномерных интегральных уравнений Фредгольма 2-го рода, основанный на специальном способе замены ядра на вырожденное. [22]
ПОЛОС МЕТОД - метод приближенного решения одномерных интегральных уравнений Фредгольма 2-го рода, основанный на специальном способе замены ядра на вырожденное, на получении резольвенты вырожденного уравнения и последующем уточнении приближенного решения с помощью быстросходящегося итеративного алгоритма. [23]
Для решения интегральных уравнений используется также метод моментов, основанный на использовании метода Бубнова - Галершша, Здесь, как и при замене ядра вырожденным, для приближения решения строится аппроксимирующая система функций. [24]
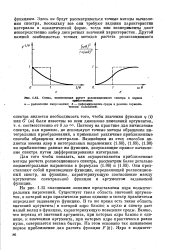 |
Схема, поясняющая расчет релаксационного спектра в первом. [25] |
Поэтому на практике для вычисления спектра, как правило, не используют точные методы обращения интегральных преобразований, а применяют различные приближенные способы обращения интегралов. Важнейшим из этих способов является замена ядер в интегральных выражениях (1.86), (1.89), (1.90) на приближенно равные им функции, допускающие прямое вычисление спектра путем дифференцирования интегралов. [26]
Для решения интегральных уравнений используется также метод моментов, основанный на использовании метода Галеркина. Здесь, как и при замене ядра вырожденным, для приближения решения строится аппроксимирующая система функций. Минимизация невязки аппроксимирующего уравнения проводится путем ее ортогонализации к базисным функциям. [27]
Из приведенного краткого обзора различных факторов, вызывающих повышение величины коэффициентов релаксационной эффективности парамагнитных ионов, видны большие возможности изменения чувствительности метода. Наибольший эффект, на наш взгляд, следует ожидать при замене ядер, на которых ведется наблюдение, и при увеличении контактного вклада в релаксацию, что достигается изменением состава раствора. При этом в ряде случаев целесообразно при определении малых количеств парамагнитных ионов измерять скорость спин-спиновой релаксации. [28]
Несколько более подробно рассмотрены уравнения с интегралами, имеющими фиксированные границы интегрирования. Для них были избраны два метода: метод квадратур и метод замены ядра уравнения / С ( х, s) на так называемое вырожденное ядро. [29]
Задача численного решения уравнений Фредгольма является более сложной, чем для уравнений Вольтерра, и имеет значительно более развитую теорию. В книге будут рассмотрены только два метода: метод квадратур и метод замены ядра уравнения на вырожденное ядро. [30]
Страницы: 1 2 3