Определенный запас - устойчивость
Cтраница 3
 |
Прямые показатели качества регулирования. [31] |
Запас устойчивости гарантирует устойчивость реальной АСР. АСР, производится с помощью критериев устойчивости. Как правило, требуется знать область изменения одного или нескольких параметров АСР, вну три которой система обладает определенным запасом устойчивости. Так, на диаграмме Вышнеградского ( рис. 14 - 2) выделены области устойчивости / /, / / /, IV. Форма задания запаса устойчивости и методика построения областей с заданным запасом устойчивости определяются используемым критерием устойчивости. [32]
В соответствии с задачей, для решения которой предназначены системы программного регулирования. Величина о6ст характеризует установившиеся режимы работы систем программного регулирования, Ндин - режимы переходных процессов в системе. Необходимым условием успешной работы системы программного регулирования, как и любой системы автоматического регулирования, является устойчивость системы и обладание ею определенным запасом устойчивости. [33]
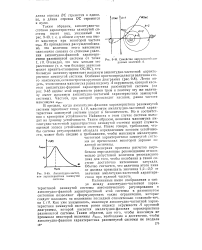 |
Семейство окружностей для разных значений А.| Амплитудно-частотная характеристика замкнутой системы. [34] |
В пределе, когда амплитудно-фазовая характеристика разомкнутой системы пересекает точку 1 10, максимум амплитудно-частотной характеристики замкнутой системы уходит в бесконечность. Но в соответствии с критерием устойчивости Найквиста в этом случае система выходит на границу устойчивости. Таким образом, величина максимума амплитудно-частотной характеристики замкнутой системы может служить оценкой запаса устойчивости системы. Иначе говоря, требование, чтобы система регулирования обладала определенным запасом устойчивости, может быть сведено к требованиям, чтобы максимум амплитудно-частотной характеристики замкнутой системы не превосходил некоторой заранее заданной величины. [35]
У несвободных стержневых систем опорные связи препятствуют появлению изгибных форм и для точного определения критических сил необходимо учитывать деформацию растяжения-сжатия в условиях продольно-поперечного и статического изгибов. Данная проблема сводится к аналитическому решению соответствующих нелинейных дифференциальных уравнений, что, в свою очередь, имеет трудности математического порядка. Поэтому обычно при определении критических сил несвободных систем продольными перемещениями ( деформациями растяжения-сжатия) пренебрегают. Полученные при этом критические силы точными методами ( методы сил, перемещений, начальных параметров, МГЭ) будут заниженными по отношению к действительному спектру. В этом состоят трудности расчета статическим методом несвободных систем на устойчивость. Однако подобные расчеты выполняются, так как критические силы будут иметь определенный запас устойчивости. Рассмотрим примеры определения критических сил несвободных рам. [36]
У несвободных стержневых систем опорные связи препятствуют появлению изгибных форм и для точного определения критических сил необходимо учитывать деформацию растяжения-сжатия в условиях продольно-поперечного и статического изгибов. Данная проблема сводится к аналитическому решению соответствующих нелинейных дифференциальных уравнений, что, в свою очередь, имеет трудности математического порядка. Поэтому обычно при определении критических сил несвободных систем продольными перемещениями ( деформациями растяжения-сжатия) пренебрегают. Полученные при этом критические силы точными методами ( методы сил, перемещений, начальных параметров, МГЭ) будут заниженными по отношению к действительному спектру. В этом состоят трудности расчета статическим методом несвободных систем на устойчивость. Однако подобные расчеты выполняются, так как критические силы будут иметь определенный запас устойчивости. Рассмотрим примеры определения критических сил несвободных рам. [37]
Вопросам устойчивости принадлежит большое место в инженерных расчетах. Идеализированная машина или конструкция, проектируемая инженером, отличается от реального объекта. Это отличие обусловлено многочисленными более или менее мелкими отклонениями от проекта, дефектами и несовершенствами. Инженеру необходима уверенность в том, что, несмотря на наличие этих отклонений, реальный объект будет работать примерно так же, как и соответствующая расчетная модель. Нетрудно видеть, что именно здесь используется концепция устойчивости. Если же малые несовершенства вызовут несопоставимо большие отклонения, то равновесие ( движение) будет неустойчивым. Конструктор или проектировщик должен выбрать параметры объекта таким образом, чтобы при всех возможных комбинациях нагрузок его равновесие ( движение) оставалось устойчивым по отношению ко всем видам возмущений, которые могут встретиться, и, более того, чтобы обеспечивался определенный запас устойчивости. [38]
Вопросам устойчивости принадлежит видное место в инженерных расчетах. Идеализированная конструкция, проектируемая инженером, отличается от осуществляемой по этому проекту реальной конструкции. Это отличие обусловлено многочисленными более или менее мелкими отклонениями от проекта, дефектами и несовершенствами. Инженеру необходима уверенность в том, что, несмотря на наличие этих отклонений, реальная конструкция будет работать примерно так же, как и соответствующая ей идеализированная конструкция. Нетрудно видеть, что именно здесь используется концепция устойчивости. Равновесие или движение проектируемой конструкции будет устойчиво, если малые несовершенства и дефекты, малые отклонения от расчетной схемы вызовут малые отклонения от идеализированных условий работы. Если же малые несовершенства вызовут несопоставимо большие отклонения, то равновесие ( движение) будет неустойчивым. Проектировщик должен выбрать размеры конструкции таким образом, чтобы при всех возможных комбинациях нагрузок равновесие ( движение) конструкции оставалось устойчивым по отношению ко всем видам возмущений, которые могут встретиться, и, более того, чтобы обеспечивался определенный запас устойчивости. [39]
Страницы: 1 2 3