Принцип - больцман
Cтраница 1
Принцип Больцмана устанавливает новый взгляд на второе начало термодинамики. [1]
Принцип Больцмана исходит из представлений о линейном вязкоупругом материале, подвергнутом в момент времени t0 бесконечно малой деформации. [2]
Обычно принцип Больцмана записывают, полагая, что набор состояний системы является дискретным. Тогда S klnQ, где Q - число микросостояний, которыми реализуется данное макросостояние. В статистической механике даются и другие определения энтропии. Как соотносятся различные определения для равновесных систем, будет рассмотрено позднее. [3]
Универсальность принципа Больцмана связана прежде всего с общностью предпосылок, заложенных в нем. Во-вторых, причина является накопленной суммой независимых следствий, действующих на каждом бесконечно малом промежутке времени. Последнее предположение во многих случаях может быть принято как исходная аппроксимация для феноменологического описания. [4]
Согласно принципу Больцмана ( см. стр. [5]
Согласно принципу Больцмана, наиболее вероятное ( равновесное) состояние наиболее устойчиво, следовательно, степень отклонения от наиболее вероятной функции F, описывающей какое-либо макроскопическое свойство системы, является мерой ее неравновесности. Указанный выше подход был применен к моделированию экологической системы водоемов, в том числе и океанов и ряда социумов. В качестве F - функции анализировалась функция распределения биомассы живого вещества, которая, как оказалась, имеет пуассоновский характер для всех водоемов, без исключения. Удалось показать неравновесный - характер экосистемы Черного моря по сравнению с Мировым океаном и неравновесный характер экономики России. Аналогично проводилось исследование плазмохимических систем, действующих в области температур 1000 - 1500 К. [6]
Согласно принципу Больцмана ( см. гл. [7]
Согласно принципу Больцмана в формулировке Планка ( см. гл. [8]
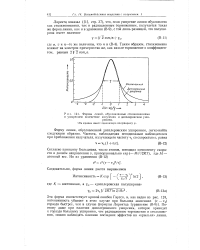 |
Формы линий, обусловленные столкновениями и уширением вследствие излучения и допплеровским уширением. Обе кривые имеют одинаковую полуширину Y. [9] |
Согласно принципу Больцмана, число атомов, имеющих компоненту скорости в данном направлении v, пропорционально ехр ( - Mu2 / 2RT), где М - атомный вес. [10]
Предложена интерпритация принципа Больцмана как устойчивость наиболее вероятного состояния. Агласно принципу Больцмана, наиболее вероятное ( равновесное) состояние / изолированной системы наиболее устойчиво. [11]
Равенство (35.1) выражает принцип Больцмана. [12]
Предположим, что принцип Больцмана сохраняет свою силу и для частиц, энергия которых квантуется. [13]
Предположим, что принцип Больцмана сохраняет свою силу и для частиц, энергия которых квантуется. Пусть мы имеем совокупность невзаимодействующих атомов, электронные оболочки которых могут находиться в состояниях, характеризуемых квантовыми числами п с энергией еп. [14]
Равенство (35.1) выражает принцип Больцмана. [15]
Страницы: 1 2 3 4