Принцип - больцман
Cтраница 3
Равновесное давление над n - м слоем ( последним слоем) рп будет по принципу Больцмана экспоненциально изменяться с изменением энергии связи этого слоя. [31]
При чисто механических движениях энтропия остается все время постоянной ( в действительности, согласно принципу Больцмана, она равна нулю; см. § 5), при термодинамических же процессах энтропия системы может меняться. Говоря об обратимом процессе, мы имеем в виду, что это изменение в любой момент в точности компенсируется противоположным по знаку изменением энтропии окружающих систему тел. [32]
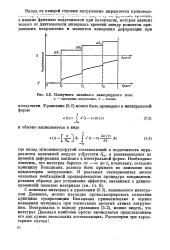 |
Ползучесть линейного вязкоупругого тела. [33] |
Необходимо отметить, что интеграл берется от - оо до t, поскольку, согласно принципу Больцмана, должна быть принята во внимание вся предыстория нагружения. В реальных экспериментах может оказаться необходимой предварительная процедура кондиционирования образца для устранения эффектов, связанных с длинно-временной памятью материала ( см. гл. [34]
Формула (17.26) является основной в квазитермодинамической теории флуктуации и, как легко видеть, непосредственно связана с принципом Больцмана для вероятностей различных макросостояний изолированной системы. [35]
Небезынтересно отметить, что мы пришли к знаменитой задаче об определении вида функции, связывающей энтропию с вероятностью, на основании принципа Больцмана, согласно которому энтропия есть функция вероятности. [36]
Последняя может быть определена приближенным образом по методу Кирквуда, описанному в § 5 и основанному на не вполне безупречном применении принципа Больцмана. [37]
Если вязкоунругий материал подвергается серии последовательных воздействий и результат каждого последующего воздействия не зависит от предыдущего, то, в соответствии с суперпозиции принципом Больцмана, деформации ( или напряжения) связаны с предысторией пагружения ( или деформирования) Больцмана - Воль-терры уравнениями. [38]
Если вязкоупругий материал подвергается серии последовательных воздействий и результат каждого последующего воздействия не зависит от предыдущего, то, в соответствии с суперпозиции принципом Больцмана, деформации ( или напряжения) связаны с предысторией нагружения ( или деформирования) Больцмана - Волъ-терры уравнениями. [39]
Этот результат является выводом фундаментального значения в статистике и служит ключом к пониманию подлинного смысла второго начала термодинамики, поэтому приведенное положение часто называют принципом Больцмана. [40]
Оставим, однако, пока в стороне вопрос о том, что мог сделать Планк и чего он не сделал, и вернемся к его неортодоксальному подходу к принципу Больцмана. Но Больцман определял наиболее вероятный способ, которым заданное число различимых молекул газа с фиксированной полной энергией может быть распределено по ячейкам фазового пространства. [41]
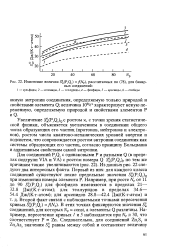 |
Изменение величин 5 ( P. QV f ( NP, рассчитанных по ( 78, для бинарных соединений. [42] |
Увеличение Sat ( PvQ) Q с ростом к, с точки зрения статистической физики, объясняется увеличением в соединении общего числа образующих его частиц ( протонов, нейтронов и электронов), ростом числа квантово-механических уровней энергии и подсистем, что сопровождается ростом энтропии соединения как системы образующих его частиц, согласно принципу Больцмана и аддитивным свойствам самой энтропии. [43]
Принцип суперпозиции Больцмана сводится к предположению о том, что все воздействия на среду независимы и аддитивны, причем ее реакция на эти воздействия линейна. Принцип Больцмана представляет основу определения понятия о линейной вязкоупругой среде. [44]
Размерные спектры ( PC), предложены Ю.Г. Камениром [12] и представляют собой функцию распределения биомассы всей совокупности популяций животных и растительных сообществ, населяющих водоем, по их усредненным линейным геометрическим размерам. Применение принципа Больцмана к водным экосистемам заключается в исследовании отклонения наиболее вероятного функционала F ( R), описывающего распределение биомассы в размерных спектрах ( PC) от распределения, наблюдаемого в природе. [45]
Страницы: 1 2 3 4