Принцип - наименьшее принуждение
Cтраница 3
Наглядными примерами приложения равновесной термодинамики к процессам поведения живых существ является эффективное использование принципа Ле Шателье-Брауна. Этот общеизвестный принцип, применимый к квазизакрытым биосистемам любой природы и иерархичности, называют принципом наименьшего принуждения и в упрощенном варианте часто формулируют следующим образом: поведенческие реакции закрытой ( квазизакрытой) системы направлены на компенсацию внешнего возмущения. [31]
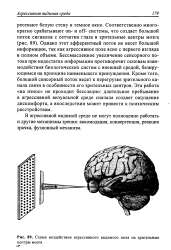 |
Схема воздействия агрессивного видимого поля на зрительные. [32] |
Однако этот афферентный поток не несет большой информации, так как агрессивное поле ясно с первого взгляда в полном объеме. Бессмысленное увеличение сенсорного потока при недостатке информации противоречит основам взаимодействия биологических систем с внешней средой, базирующимся на принципе наименьшего принуждения. Кроме того, большой сенсорный поток ведет к перегрузке зрительного канала связи в особенности его зрительных центров. Эта работа на износ не проходит бесследно: длительное пребывание в агрессивной визуальной среде сначала создает ощущение дискомфорта, а впоследствии может привести к психическим расстройствам. [33]
В настоящем разделе мы исследуем подход, который основан на ином принципе управления процессом рассуждений - на так называемом принципе наименьшего принуждения. Главная идея состоит в том, что решения не должны приниматься необосновано или поспешно. Они должны откладываться до тех пор, пока не будет достаточно информации для их принятия. [34]
Все принципы по форме своей разделяются на две категории: на принципы дифференциальные и интегральные. К первым относятся: принцип Даламбера ( D Alembert), принцип виртуальных перемещений [ принцип Лагранжа ( Lagrange) J, принцип наименьшего принуждения. [35]
Все принципы по форме своей разделяются на две категории: на принципы дифференциальные и интегральные. К первым относятся: принцип Даламбера ( D Alembert), принцип виртуальных перемещений [ принцип Лаграижа ( Lagrange) J, принцип наименьшего принуждения. [36]
В своей формулировке: каждое естественное движение самостоятельной материальной системы состоит в том, что система движется с постоянной скоростью по одному из своих прямейших путей, Герц объединяет, по существу говоря, закон инерции и принцип наименьшего принуждения. Герц отмечает глубокую связь своего принципа с теорией поверхностей и многочисленные аналогии, которые возникают при его рассмотрении. Принцип Герца находится в тесной связи с геометрической оптикой и теоремой Бельтрами - Липшица, так как между прямейшими путями и нормальными к ним поверхностями в процессе движения имеет-место то же соотношение, что и между лучами и волновыми поверхностями. Герц полностью исключил всякие теологические умозаключения из своего, принципа, так как в нем настоящее не определяется через будущее. Сам Герц показал, что принцип прямейшего пути непосредстенно связан с принципом, наименьшего действия в форме Якоби и с принципом Гамильтона. [37]
Если дело доходит до выполнения операций третьей группы, то сначала программа пытается устранить нарушение наиболее существенного ограничения. Таким образом, одно из важнейших отличий программы VT от MOLGEN состоит в том, что хотя в обеих системах используется стратегия предложение и пересмотр, в программе VT гораздо большее внимание уделено фазе пересмотра ранее принятых решений, а программа MOLGEN концентрируется на реализации принципа наименьшего принуждения. [38]
Четвертая из перечисленных выше особенностей иллюстрирует интересное ограничение принципа наименьшего принуждения. Каждый решатель задач имеет только частичное знание о решении задач в некоторой проблемной области. При использовании одного лишь принципа наименьшего принуждения процесс решения должен приводить к останову всякий раз, когда имеется некоторый набор решений, которые можно принять, но отсутствуют достаточные основания для принятия какого-либо из них. Мы называем эту ситуацию тупиковой. Обнаружив такую ситуацию, MOLGEN переключается на эвристический метод и выдвигает некоторую гипотезу. [39]
Вполне очевидно, что такая формулировка, по существу, охватывает принцип стабильности. В простейших случаях принцип Ле Шателье просто эквивалентен условиям стабильности. В таком контексте принцип Ле Шателье практически дублирует принцип наименьшего принуждения, сформулированный еще в работах Да-ламбера и Гаусса. Однако ограниченность данной формулировки с-позиций химической термодинамики может в ряде случаев привести к совершенно неправильным заключениям. [40]
Метод последовательной детализации сверху вниз не учитывает изменчивость в подготовленности принимать решения. В седьмом случае мы ввели принцип наименьшего принуждения, согласно которому принятие решений должно быть отсрочено до тех пор, пока не будет достаточно информации для их принятия. Было введено предположение, что принципы, подобные принципу наименьшего принуждения, должны быть включены как часть метауровня решения задач. [41]
Несомненно также, что он целиком согласуется с общими идеями саморегуляции, разрабатываемыми в технике и кибернетике, где мы находим многочисленные модификации этого принципа, например, принцип наименьшего взаимодействия - для объяснения работы нервных центров [8] или принцип наименьшего принуждения [9], призванного объяснить деятельность всех адаптивных систем - живых, социальных и технических. [42]
При помощи вариаций особого вида Гауссу удалось преобразовать принцип Даламбера в подлинно минимальный принцип, в котором отыскивается минимум некоторой скалярной величины, названной Гауссом мерой принуждения; при этом ускорения рассматриваются как переменные вариационной задачи. Будучи принципом минимума, принцип наименьшего принуждения аналогичен принципу наименьшего действия. Он проще, чем этот последний, так как не требует вариационного исчисления, поскольку отыскивается не минимум определенного интеграла, а минимум обычной функции. Большим недостатком принципа наименьшего принуждения является то, что он требует вычисления ускорений. Это, вообще говоря, приводит к гораздо более громоздким и трудоемким вычислениям. В то же время в принципе наименьшего действия все выводится - из скалярной функции, не содержащей производных выше первого порядка. [43]
В аналитической механике этот метод приводит к новому общему принципу. В 1829 г. Карл Фридрих Гаусс ( 1777 - 1855) опубликовал свой знаменитый мемуар, в котором предложил доказательство принципа наименьшего принуждения. [44]
Для систем с линейными неголономными связями принцип Гаусса можно вывести из принципа Даламбера - Лагранжа, предполагая, что эти связи являются идеальными. Но в случае неголономных связей общего вида этого сделать нельзя, не зная структуры связей или, точнее, не установив, по отношению к каким перемещениям системы эти связи являются идеальными. Поэтому нельзя утверждать, что принцип Гаусса применим ко всякой неголономной системе. Целью настоящей работы является выяснение вопроса, какому условию должны удовлетворять реакции неголономных нелинейных связей, чтобы для системы с такими связями был справедлив принцип наименьшего принуждения. [45]
Страницы: 1 2 3 4