Принцип - симметрия
Cтраница 2
Принципом симметрии Римана - Шварца называется один частный способ аналитического продолжения, замечательный своей простотой. Он имеет большое значение в теории конформных отображений. [16]
Применяя принцип симметрии, построим систему многоугольников, каждый из которых является изображением относительно его сторон прилежащих к нему многоугольников. Так как многоугольники поочередно являются отображениями верхней и нижней полуплоскости ( w), то из двух соседних многоугольников, прилежащих к одной стороне, один является отображением верхней полуплоскости, а другой - нижней полуплоскости. [17]
Сформулировать принцип симметрии для продолжения источника тепла через прямолинейный или круговой участок границы области. Найти распределение температуры в произвольной односвязной области D, если известно, что внутри этой области находится источник ( a; q) и температура на границе имеет постоянное значение С. [18]
Применяя принцип симметрии, мы увидим, что эта же функция будет отображать взаимнооднозначно и конформно внутренность всего эллипса на плоскость, разрезанную вдоль некоторого отрезка действительной оси. Остается затем лишь преобразовать эту разрезанную плоскость в верхнюю полуплоскость, чтобы иметь взаимно однозначное и-конформное отображение внутренности всего эллипса на верхнюю полуплоскость. [19]
Используя принципы симметрии, рассмотренные в разделе В, с гл. II, покажите, что маг-пи Шый момент для перехода Л, - ои Е бензоле равен нулю. [20]
Используя принцип симметрии, распространим течение на всю плоскость. Тогда при зеркальном отображении через окружность нули переходят в полюсы, а при отображении через вещественную ось ( диаметр) нули переходят в нули. [21]
Применяя принцип симметрии, мы увидим, что эта же функция будет отображать взаимно однозначно и конформно внутрен-ность всего эллипса на плоскость, разрезанную вдоль некоторого отрезка действительной оси. Остается затем лишь преобразовать эту разрезанную плоскость в верхнюю полуплоскость, чтобы иметь взаимно однозначное и конформное отображение внутренности всего эллипса на верхнюю полуплоскость. [22]
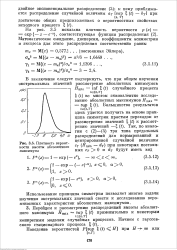 |
Плотность вероятности высоты абсолютного максимума. [23] |
Использование принципа симметрии позволяет многие задачи изучения экстремальных значений свести к исследованию вероятностных характеристик абсолютных максимумов. [24]
Из принципа симметрии следует, что при наличии прямолинейного или кругового участка на линии тока или эквипотенциальной линии течение должно быть симметричным относительно этой линии. [25]
Кроме принципа симметрии, связанного с положениями об инвариантности ( неизменности), существует принцип относительности ( не абсолютности), базирующийся на отказе от признания возможности установить какую-либо абсолютную систему отсчета для времени, пространства и направлений в пространстве; в мире нет нулевой точки для времени ( он вечен), нет нулевой точки или абсолютной нулевой оси, от которой можно было бы откладывать углы при вращении этой оси. [26]
 |
Схема измерения утечек для транзистора типа р-п - р. [27] |
Использование принципа симметрии для измерения токов утечки возможно только для транзисторов, для которых выполняется принцип взаимности. [28]
Из принципа симметрии Шварца ( см. [33]) следует, что М 1 и 1 ( х) - сопряженные функции. [29]
Из принципа симметрии Шварца вытекает, что их мнимые части в этнх точках отличаются знаком. [30]
Страницы: 1 2 3 4