Прогиб - оболочка
Cтраница 2
Начиная с некоторого времени t гкр, амплитуда прогиба оболочки растет и она теряет устойчивость. [16]
Единственное отличие вносится в данном случае тем, что прогибы оболочки определяются в функции уже не одного, а двух независимых переменных. [17]
Техническая теория оболочек используется при среднем изгибе [2.7], когда прогибы оболочки сравнимы с ее толщиной. [18]
Подстановка этого значения в выражение ( 1) позволит нам вычислить прогиб оболочки в любой ее точке. [19]
Здесь следует отметить, что нарастающая амплитуда колебаний довольно быстро превосходит стационарный прогиб оболочки. Процесс движения представляет собой нестационарные колебания около нулевой линии, по мере развития которого различия прогибов становятся значительными. Для реальных конструкций это означает возможность расслоения. [20]
В формуле ( 28) слагаемое, содержащее cos ф, выражает прогиб оболочки как балки. [21]
При m 10, что соответствует 21 стрингеру в фиктивной оболочке, прогиб действительной оболочки будет в первом и во втором случаях соответственно на 7 и 1 % больше прогиба фиктивной оболочки. [22]
Для изучения гибких упругопластических оболочек этот подход реализован в [113], где в качестве параметра введен прогиб оболочки в центре, что позволило исключить трудности получения решения в окрестности предельных точек. Для-их прямого определения ( без построения траектории состояний равновесия) проведено продолжение решения по геометрическому параметру подъемистости оболочки, система уравнений равновесия дополнена уравнением det ( /) 0, где / - матрица линеаризованной системы алгебраических уравнений, полученной методом Ритца. [23]
Для того чтобы придать им определенные значения, мы будем исходить из предположения, что периодичность прогибов оболочки сохраняется при закритической деформации и такая же, как в момент потери устойчивости. [24]
Из исследований выяснено, что в приопорных полосовых зонах происходит местное искривление срединной поверхности оболочки и наблюдается заметный прогиб оболочки, уменьшающийся до нуля над контурными конструкциями. Таким образом, в приконтурных полосовых зонах происходит местный изгиб оболочки. Здесь возникают изгибающие моменты, действующие в направлении, перпендикулярном контуру. [25]
J / R3h достаточно велика, так как в противном случае не выполняется предположение о более медленной изменяемости прогибов оболочки в окружном направлении по сравнению с меридиональным. В этом случае с ростом k слагаемые сначала растут, а затем быстро убывают. [26]
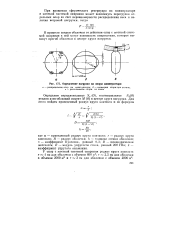 |
Определение нагрузки на опоры манипулятора. [27] |
В процессе сварки оболочки от действия опор с жесткой системой опирания в ней могут возникнуть напряжения, которые вызовут прогиб оболочки в центре круга нагрузки. [28]
В этой главе мы рассмотрим применение методов предыдущей главы к нелинейным краевым задачам, описывающим большие прогибы арок и большие осесимметрические прогибы оболочек вращения. Имея в виду, что нашей основной целью является демонстрация алгоритмов продолжения решения, мы остановились на случае малых упругих деформаций без ограничений на углы поворота оси арки и срединной поверхности оболочки. [29]
Задача определения критического параметра t при этом сводится к нахождению наибольшего собственного числа матрицы А, вектор С позволяет определить прогибы оболочки. Основная трудность, которая при этом возникает, - это выбор чисел т, п, соответствующих главным членам ряда. Дело в том, что при сильной изменяемости исходного напряженного состояния форма потери устойчивости имеет большую неоднородность. Для ее описания в ряде требуется удерживать большое количество членов, причем главные члены ряда зачастую лежат далеко от его начала, так что нельзя взять достаточное число членов в порядке возрастания т, п от начала ряда: порядок матрицы А при этом был бы очень высоким даже для современных вычислительных машин. Из системы (3.18) видно, что при постоянных большая величина К соответствует меньшим ат. Поэтому разумно за главные члены ряда взять такие, которые соответствуют меньшим ат. [30]
Страницы: 1 2 3 4