Прогиб - оболочка
Cтраница 3
Аналогичное исследование уравнения равновесия в радиальном направлении (4.5.4.41) с использованием уравнений (4.5.4.62), (4.5.4.58) и (4.5.4.59) позволяет выписать основное дифференциальное уравнение для прогиба оболочки, из решения которого могут быть найдены все напряжения. [31]
 |
Построение матрицы для определения постоянных в однородном решении уравнений для длинных и коротких цилиндрических оболочек. [32] |
Если края цилиндрической оболочки достаточно удалены друг от друга, то они не оказывают существенного влияния друг на друга; в этом случае прогибы оболочки могут быть представлены краевыми функциями, затухающими по мере удаления от краев. [33]
Усматриваемое из графиков нарушение условия непроникновения ( см. (15.78) 4), которое ( нарушение) выражается в том, что на некоторых участках прогиб оболочки превышает прогиб кольца, является следствием погрешности вычисления прогибов кольца по найденным итерационным путем реакциям. [34]
Так, например, при т 3, что соответствует семи фиктивным стрингерам в сечении оболочки, в первом случае, когда все стрингера одинаковы, прогиб действительной оболочки в плоскости уг оказывается в 1 51 больше прогиба подкрепленной фиктивной оболочки, и во втором случае, когда крайние стрингера имеют площади поперечных сечений в 2 раза меньшие по сравнению с остальными стрингерами, прогиб гладкой оказывается в 1 21 больше прогиба заменяющей ее фиктивной оболочки. При т 5, что соответствует 11 фиктивным стрингерам в оболочке, прогиб фиктивной оболочки оказывается в первом случае в 1 32 и во втором в 1 07 больше прогиба действительной гладкой оболочки. [35]
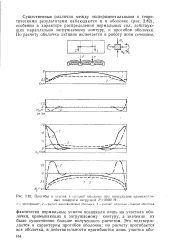 |
Прогибы и усилия в средней оболочке при нагружении промежуточных диафрагм нагрузкой Р 2000 Н. 1 - эксперимент. 2 - расчет многоволновых оболочек. 3 - расчет отдельно стоящей оболочки. [36] |
Существенные различия между экспериментальными и теоретическими результатами наблюдаются и в оболочке ( рис. 2.82), особенно в характере распределения нормальных сил, действующих параллельно загружаемому контуру, и прогибов оболочки. [37]
При m 10, что соответствует 21 стрингеру в фиктивной оболочке, прогиб действительной оболочки будет в первом и во втором случаях соответственно на 7 и 1 % больше прогиба фиктивной оболочки. [38]
Прогиб включает в себя ( см. рис. 5.8): бц - перемещение точки А витка относительно точки 0 в его основании вследствие деформации изгиба и сдвига; 612 - прогиб оболочки в результате поворота основания витка; 6i3 - осевое перемещение точки А витка в оезультате изгиба оболочки. [39]
Формулой (7.85) можно пользоваться только в том случае, если относительная жесткость шпангоута JIR h достаточно велика, так как в противном случае не выполняется предположение о более медленной изменяемости прогибов оболочки в окружном направлении по сравнению с меридиональным. Обратим внимание на характер изменения членов ряда (7.85) в зависимости от k при малых значениях JIRzh. В этом случае с ростом k слагаемые сначала растут, а затем быстро убывают. [40]
Наряду с проверкой по этому критерию на каждом шаге по внешним воздействиям ( при исследовании устойчивости в упругой области) и по времени ( при исследовании устойчивости при ползучести) осуществляем контроль за скоростью изменения прогиба оболочки по ведущему параметру. [41]
Так, например, при т 3, что соответствует семи фиктивным стрингерам в сечении оболочки, в первом случае, когда все стрингера одинаковы, прогиб действительной оболочки в плоскости уг оказывается в 1 51 больше прогиба подкрепленной фиктивной оболочки, и во втором случае, когда крайние стрингера имеют площади поперечных сечений в 2 раза меньшие по сравнению с остальными стрингерами, прогиб гладкой оказывается в 1 21 больше прогиба заменяющей ее фиктивной оболочки. При т 5, что соответствует 11 фиктивным стрингерам в оболочке, прогиб фиктивной оболочки оказывается в первом случае в 1 32 и во втором в 1 07 больше прогиба действительной гладкой оболочки. [42]
Рассмотрим упругую цилиндрическую панель, опертую на прямоугольный в плане контур. Предположим, что прогибы оболочки сопоставимы с ее толщиной, хотя и малы по сравнению с другими линейными размерами. Будем считать, что при этом выполняется гипотеза Кирхгофа - Лява. [43]
Существо дела здесь состоит в следующем, Пусть, к примеру, на оболочку типа сферического купола действует постоянное внешнее давление. За счет ползучести прогибы оболочки растут, но скорость этого роста затухает, и этот процесс деформирования до некоторых значений нагрузок будет устойчивым на бесконечном интервале времени по отношению к малым возмущениям. [44]
 |
Диаграмма нагрузка - амплитуда прогиба для проектов 1 и 2 ( 2 0. [45] |
Страницы: 1 2 3 4