Прогнозирование - временной ряд - Большая Энциклопедия Нефти и Газа, статья, страница 1

Прогнозирование - временной ряд

Cтраница 1

Прогнозирование временных рядов является инструментом для определения тенденций изменения атрибутов рассматриваемых объектов с течением времени. Анализ поведения временных рядов позволяет прогнозировать значения исследуемых характеристик. [1]

При прогнозировании временных рядов часто в распоряжении исследователей имеется априорная информация о значениях временного ряда в будущие моменты времени, для которых и производится прогноз. Ясно, что при решении практических задач априорная информация в абсолютном большинстве случаев носит неопределенный характер. В таких ситуациях задача прогнозирования состоит в оптимальном учете априорной информации при ее объединении в процессе прогнозирования с информацией, содержащейся в уже реализованной части временного ряда. [2]

Использование для целей прогнозирования временных рядов изменения расхода электроэнергии ( трендовые и авторегрессионные модели) неоправданно, так как описание тенденции изменения только с помощью функции времени означает, что время единственная причина изменения электропотребления. На самом деле развитие того или иного явления определяется множеством внутренних причин и фактор времени аккумулирует их влияние, поэтому модель тренда не вскрывает причин изменения, а носит чисто описательный характер. [3]

Сегодня наиболее применяемым методом прогнозирования временных рядов является экстраполяционный метод прогнозирования. [4]

В качестве тестовой рассмотрена задача прогнозирования многомерного временного ряда. В качестве архитектуры взята многослойная нейронная сеть с различными критериями и алгоритмами обучения. [5]

Главы 11, 12 посвящены анализу и прогнозированию временных рядов. Все представленные в главе методы основаны на представлении детерминированной компоненты в виде разложения по базисной системе функций и оценке коэффициентов разложения с помощью МНК или робастной схемы. В качестве базисной системы функций берутся: 1) система полиномов, ортогональных на множестве фиксированных значений аргумента; 2) линейные сплайны; 3) кубические сплайны; 4) вейвлеты. Предлагаются эффективные численные схемы расчета искомых коэффициентов детерминированных компонент. Первые два из них основаны на учете априорных экспертных оценок прогнозируемых величин и применении схем выделения детерминированных компонент, изложенных в гл. [6]

Данное соотношение может быть использовано для решения задачи прогнозирования временного ряда. [7]

Окно задания параметров обучения. [8]

Отдельная опция Random Last examples введена для задач прогнозирования временных рядов. При этом последние примеры всегда исключаются из обучения и являются, по сути, прогнозом. [9]

Схема возникновения русла. В некоторой области G различные траектории могут оказаться близкими в проекции. Тогда в этой проекции динамика становится частично предсказуемой. Однако такая модель в проекции будет иметь принципиально ограниченную точность. Ситуация похожа на использование методов усреднения, когда усредненная модель получается как проекция на подпространство медленно меняющихся мод. Однако, в отличие от них, здесь модель справедлива только при попадании траектории в область G. Как только траектория исходной системы покинет эту область, предсказуемость в проекции будет утрачена. [10]

Рассмотрим теперь, как идею русел можно применить для прогнозирования временных рядов. [11]

На четвертом-шестом уровнях также предлагается определять расчетные нагрузки путем прогнозирования временных рядов отчетных электрических показателей. [12]

Выполненные мной во время войны работы по фильтрации и прогнозированию временных рядов представляли собой непосредственное продолжение моих ранних работ по теории брауновского движения и изучению беспорядочных колебаний во времени при помощи аппарата обобщенного гармонического анализа. [13]

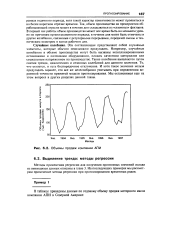Объемы продаж компании АПИ. [14]

На последующих примерах мы рассмотрим применение метода регрессии при прогнозировании временных рядов. [15]

Страницы: 1 2 3